《2025年同步练习册泰山出版社七年级数学上册青岛版》

6. 如图,编写了计算机的运算程序,若开始输入$x = -1$,则最后输出的结果是-5。

答案： -5

7. 利用乘法运算律进行简便计算：
(1)$(-4)×8×(-2.5)×(-125)$；
(2)$(-\frac{1}{2}+\frac{1}{6}-\frac{3}{8}+\frac{5}{12})×(-24)$；
(3)$(+23)×\frac{1}{4}+(-57)×\frac{1}{4}+26×(-\frac{1}{4})$。

答案： 1. （1）
解：
利用乘法交换律$a× b = b× a$和结合律$(a× b)× c=a×(b× c)$，
$(-4)×8×(-2.5)×(-125)=[(-4)×(-2.5)]×[8×(-125)]$。
因为$(-4)×(-2.5)=10$，$8×(-125)=-1000$，
所以$10×(-1000)= - 10000$。
2. （2）
解：
利用乘法分配律$(a + b + c + d)× e=a× e + b× e + c× e + d× e$，
$(-\frac{1}{2}+\frac{1}{6}-\frac{3}{8}+\frac{5}{12})×(-24)=(-\frac{1}{2})×(-24)+\frac{1}{6}×(-24)-\frac{3}{8}×(-24)+\frac{5}{12}×(-24)$。
计算各项：
$(-\frac{1}{2})×(-24)=12$，$\frac{1}{6}×(-24)=-4$，$-\frac{3}{8}×(-24)=9$，$\frac{5}{12}×(-24)=-10$。
则$12-4 + 9-10=(12 + 9)-(4 + 10)=21 - 14 = 7$。
3. （3）
解：
利用乘法分配律$a× c + b× c=(a + b)× c$，
$(+23)×\frac{1}{4}+(-57)×\frac{1}{4}+26×(-\frac{1}{4})=(23 - 57-26)×\frac{1}{4}$。
先计算括号内：$23-57 - 26=(23-(57 + 26))=23 - 83=-60$。
再计算$-60×\frac{1}{4}=-15$。
综上，答案依次为：（1）$-10000$；（2）$7$；（3）$-15$。

8. “格子乘法”作为两数相乘的一种计算方法,在明代的《算法统宗》一书中被称为“铺地锦”。如图①,计算$47×51$,将乘数 47 计入上行,乘数 51 计入右列,然后用 47 的每位数字分别乘 51 的每位数字,将结果计入相应的格子中,最后按斜行加起来,得 2397。类比解决下列问题：
(1) 如图②,用“格子乘法”表示$25×71$,则$a = $____；
(2) 借用图②结果计算：$-5×24×(-5)×71×(-\frac{1}{12})$；
(3) 观察图③,求$mn$的值。

答案：
解:
(1)利用“格子乘法”表示即可得到a的值,如图所示:

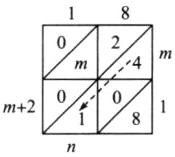
a=5+2=7,故答案为:7；
(2)根据图可知:25×71=1775，
-5×24×(-5)×71×$(-\frac{1}{12})$
=25×71×24×$(-\frac{1}{12})$
=(25×71)×[24×$(-\frac{1}{12})$]
=1775×(-2)
=-3550
(3)利用“格子乘法”表示即可得到m,n的值,则m=3，n=5,所以,mn=15。