《2025年同步练习册泰山出版社七年级数学上册青岛版》

1. $|+157|=$157；$\left|-\dfrac{3}{5}\right|=$$\frac{3}{5}$；$|-6.5|=$6.5。

答案： 157 $\frac{3}{5}$ 6.5

知识点2 绝对值的性质
思考
Ⅲ. 绝对值的性质有哪些？

答案： Ⅲ.
(1)互为相反数的两个数的绝对值相等;
(2)一个数的绝对值是正数或 0;
(3)正数的绝对值是它本身;负数的绝对值是它的相反数;0 的绝对值是 0。

2. 下列说法：①$7的绝对值是7$；②$-7的绝对值是7$；③绝对值等于$7的数是7或-7$；④绝对值最小的有理数是$0$。其中正确说法有(D)。
A.$1$个
B.$2$个
C.$3$个
D.$4$个

答案： D

3. 若$|a|= 5$,$|b|= 1$,且$a ＜ b$,求$a$,$b$的值。

答案： a=-5,b=-1 或 a=-5,b=1。

1. $-2024$的绝对值是(A)。

A.$2024$
B.$-2024$
C.$\pm2024$
D.$0$

答案： A

2. 下列各数中绝对值最小的数是(D)。
A.$-2.7$
B.$-2$
C.$7$
D.$0$

答案： D

3. 已知$|a|= -a$,则数$a$为(D)。
A.负数
B.正数
C.$0$
D.负数或$0$

答案： D

4. 已知$a= -3$,$|a|= |b|$,则$b$的值为(D)。
A.$+3$
B.$-3$
C.$0$
D.$\pm3$

答案： D

5. 如图,在数轴上$A点表示数a$,$B点表示数b$,且$a$,$b满足|a + 12|+(b - 6)^2 = 0$。

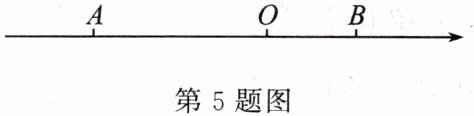
(1)求$A$,$B$两点之间的距离；
(2)点$C$,$D在线段AB$上,$AC为14$个单位长度,$BD为8$个单位长度,求线段$CD$的长。

答案： 解:
(1)因为|a+12|+(b-6)$^2$=0,所以 a+12=0,b-6=0,即 a=-12,b=6。所以 AB=OA+OB=12+6=18。
(2)点 C,D 在线段 AB 上,点 C 在 A 点的右侧,点 D 在 B 点的左侧。因为 AB=18,AC=14,BD=8,所以 CD=AC+BD-AB=14+8-18=4。

6. 根据所学的数轴知识,解答下面的问题：

【问题解决】
(1)如图,将一根木棒放在数轴(单位长度为$1cm$)上,木棒左端与数轴上的点$A$重合,右端与数轴上的点$B$重合。若将木棒沿数轴水平向右移动,则当它的左端点移动到点$B$处时,它的右端点在数轴上对应的数为$20$；若将木棒沿数轴水平向左移动,则当它的右端点移动到点$A$处时,它的左端点在数轴上对应的数为$5$,由此可得到木长为______ $cm$；数轴上点$A$表示的数为______ ,点$B$表示的数为______ ；
【类比探究】
(2)请你借助“数轴”这个工具帮助小亮解决下列问题：一天,小亮问爷爷的年龄,爷爷说：“我若是你现在这么大,你还要$30$年才出生；你若是我现在这么大,我已经$117$岁,是老寿星了,哈哈！”请求出爷爷现在的年龄。

答案：
解:
(1)5,10,15;
(2)如图,把小亮与爷爷的年龄差看作木棒 AB,
爷爷和小亮一样大时,相当于 A 点移动到 B 点,此时 B 点所对应的数为-30,小亮和爷爷一样大时,相当于 B 点移动到 A 点时,此时 A 点所对应的数为 117,所以爷爷比小亮大:[117-(-30)]÷3=49(岁),所以爷爷的年龄为 117-49=68(岁),答:爷爷现在的年龄是 68 岁。