《2025年步步高大一轮复习讲义物理教科版》

1. (2025·河北张家口市阶段测试)如图(a)所示，倾角为 $37^{\circ}$ 的传送带以 $v = 2.0\ m/s$ 的速度顺时针匀速转动，传送带的长度 $L_{AB} = 10.0\ m$。一个可视为质点的质量 $m = 1.0\ kg$ 的物块，自 $A$ 点无初速度地放在传送带底端，其被传送至 $B$ 端的过程中，动能 $E_{k}$ 与位移 $x$ 的关系 ($E_{k} - x$) 图像如图(b)所示。重力加速度 $g$ 取 $10\ m/s^2$，$\sin 37^{\circ} = 0.6$，$\cos 37^{\circ} = 0.8$。下列说法正确的是(D)

(a)
(b)

A.物块与传送带之间的动摩擦因数为 $0.25$
B.整个过程中合外力对物块做的功为 $4.0\ J$
C.整个过程中摩擦力对物块做的功为 $64.0\ J$
D.整个过程中摩擦力对物块做的功等于物块机械能的增加量

答案： 1. D [开始时物块在传送带的作用下动能不断增加，根据动能定理有$(\mu mg\cos 37° - mg\sin 37°)x = E_{k} - 0$，
![img alt=1题图]（图中为一条斜向右上的皮带，地面左高右低，左端点a右端点b，物块从a点以初速度0开始运动，速度方向向右，皮带速度向右）
在$5\ m$后动能不变，可知物块与传送带相对静止，即$v = 2.0\ m/s$，$E_{k} = \frac{1}{2}mv^{2} = 2.0\ J$，联立解得$\mu = 0.8$，A错误；由动能定理可知，整个过程中合外力对物块做的功等于物块动能的变化量，则有$W_{合} = \Delta E_{k} = \frac{1}{2}mv^{2} = 2.0\ J$，B错误；由功能关系可知，整个过程中摩擦力对物块做的功等于物块机械能的增加量，即$W_{f} = \frac{1}{2}mv^{2} + mgL_{AB}\sin 37° = 62.0\ J$，C错误，D正确。]

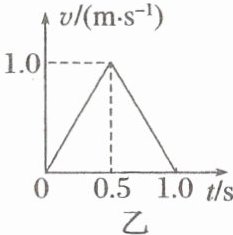
2. (多选)(2024·贵州省名校协作体三模)如图甲所示，质量为 $0.1\ kg$ 的滑块(可视为质点)在内壁光滑、固定的水平筒内压缩弹簧，弹簧原长小于筒长，且弹簧与滑块不拴接。滑块由静止释放，离开筒后立即滑上静止于水平面上的木板左端，开始计时，此后木板的 $v - t$ 图像如图乙所示。已知木板质量也为 $0.1\ kg$，木板的长度为 $1\ m$，滑块与木板间的动摩擦因数为 $0.6$，最终滑块恰好没有离开木板。忽略空气阻力，重力加速度大小取 $10\ m/s^2$。则(AB)

甲

乙

A.木板与地面之间的动摩擦因数为 $0.2$
B.木板运动 $0.5\ s$ 后与滑块达到共速
C.释放滑块时弹簧的弹性势能为 $0.6\ J$
D.木板与水平面间因摩擦产生的热量为 $0.25\ J$

答案： 2. AB [已知滑块与木板间的动摩擦因数为$\mu_{1} = 0.6$，设木板与地面之间的动摩擦因数为$\mu_{2}$，滑块刚滑上木板时，木板做匀加速直线运动，根据牛顿第二定律可得$\mu_{1}mg - \mu_{2}(M + m)g = Ma_{1}$，根据题图乙得$a_{1} = \frac{1}{0.5}\ m/s^{2} = 2\ m/s^{2}$，联立解得$\mu_{2} = 0.2$，故A正确；由$v - t$图像可知，$t_{1} = 0.5\ s$木板开始做匀减速运动，可知此时滑块刚好与木板共速，B正确；设块刚滑上木板时的速度为$v_{0}$，共速前，以滑块为研究对象，根据牛顿第二定律可得$a = \frac{\mu_{1}mg}{m} = 6\ m/s^{2}$，根据运动学公式可得$v_{共} = v_{0} - at_{1}$，可得$v_{0} = v_{共} + at_{1} = 1.0\ m/s + 6 × 0.5\ m/s = 4\ m/s$，根据能量守恒可知，释放滑块时弹簧的弹性势能为$E_{p} = \frac{1}{2}mv_{0}^{2} = 0.8\ J$，故C错误；根据$v - t$图像可知，整个过程木板通过的位移为$x = \frac{1}{2} × 1.0 × 1.0\ m = 0.5\ m$，则木板与水平面间因摩擦产生的热量为$Q = \mu_{2}(M + m)g \cdot x = 0.2\ J$，故D错误。]

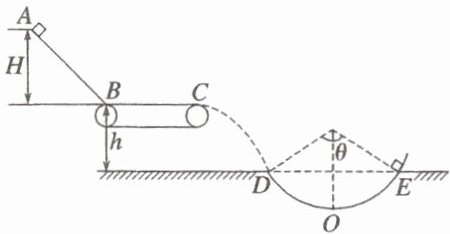
3. (14 分)(2025·江苏盐城市五校联考)如图所示，光滑斜面 $AB$ 与水平传送带 $BC$ 平滑连接，$BC$ 长 $L = 4.5\ m$，与物块间的动摩擦因数 $\mu = 0.3$，传送带顺时针转动的速度 $v = 3\ m/s$。设质量 $m = 2\ kg$ 的物块由静止开始从 $A$ 点下滑，经过 $C$ 点后水平抛出，恰好沿圆弧切线从 $D$ 点进入竖直光滑圆弧轨道 $DOE$，$DE$ 连线水平。已知圆弧半径 $R = 2.0\ m$，对应圆心角 $\theta = 106^{\circ}$，物块运动到 $O$ 点时对轨道的压力为 $61\ N$。$g$ 取 $10\ m/s^2$，$\sin 37^{\circ} = 0.6$，$\cos 37^{\circ} = 0.8$，求：
(1)(4 分)物块运动到 $D$ 点的速度大小 $v_{D}$；
(2)(6 分)物块下落的最大高度 $H$；
(3)(4 分)第(2)问中，物块与传送带间产生的热量 $Q$。

答案： 3.
(1)$5\ m/s$
(2)$1.8\ m$
(3)$9\ J$
解析
(1)物块由D点到O点根据动能定理有$mgR(1 - \cos 53°) = \frac{1}{2}mv_{D}^{2} - \frac{1}{2}mv_{0}^{2}$
在O点有$N - mg = m\frac{v_{0}^{2}}{R}$，
联立解得$v_{D} = 5\ m/s$
(2)在D点将速度沿水平方向和竖直方向进行分解，根据平抛运动的规律可得该位置物块的水平速度即为$v_{C}$，故$v_{C} = 3\ m/s$。当物块下落的最大高度为$H$时，物块在传送带上一直做匀减速直线运动到$C$点，根据牛顿第二定律有$\mu mg = ma$，得$a = 3\ m/s^{2}$
根据速度位移公式有$v_{C}^{2} - v_{B}^{2} = - 2aL$
解得$v_{B} = 6\ m/s$
从A到B根据动能定理可得$mgH = \frac{1}{2}mv_{B}^{2}$
解得$H = 1.8\ m$
(3)根据运动学知识可知$v_{C} = v_{B} - at$
解得$t = 1\ s$
所以相对位移$\Delta x = (4.5 - 3)\ m = 1.5\ m$
产生的热量$Q = \mu mg\Delta x = 9\ J$

4. (16 分)(2024·海南卷·18)某游乐项目装置简化如图，$A$ 为固定在地面上的光滑圆弧形滑梯，半径 $R = 10\ m$，滑梯顶点 $a$ 与滑梯末端 $b$ 的高度差 $h = 5\ m$，静止在光滑水平面上的滑板 $B$ 紧靠滑梯的末端，并与其水平相切，滑板质量 $M = 25\ kg$，一质量为 $m = 50\ kg$ 的游客，从 $a$ 点由静止开始下滑，在 $b$ 点滑上滑板，当滑板右端运动到与其上表面等高平台 $C$ 的边缘时，游客恰好滑上平台，并在平台上滑行 $s = 16\ m$ 停下。游客视为质点，其与滑板及平台表面之间的动摩擦因数均为 $\mu = 0.2$，忽略空气阻力，重力加速度 $g$ 取 $10\ m/s^2$，求：
(1)(7 分)游客滑到 $b$ 点时对滑梯的压力的大小；
(2)(9 分)滑板的长度 $L$。

答案： 4.
(1)$1\ 000\ N$
(2)$7\ m$
解析
(1)设游客滑到b点时速度为$v_{0}$，从a到b过程，根据机械能守恒有$mgh = \frac{1}{2}mv_{0}^{2}$
解得$v_{0} = 10\ m/s$
在b点根据牛顿第二定律$F_{N} - mg = m\frac{v_{0}^{2}}{R}$
解得$F_{N} = 1\ 000\ N$
根据牛顿第三定律得游客滑到b点时对滑梯的压力的大小为$F_{N}' = F_{N} = 1\ 000\ N$
(2)设游客恰好滑上平台时的速度为$v$，在平台上运动过程由动能定理得$-\mu mgs = 0 - \frac{1}{2}mv^{2}$
解得$v = 8\ m/s$
根据题意当滑板右端运动到与其上表面等高平台C的边缘时，游客恰好滑上平台，可知该过程游客一直做减速运动，滑板一直做加速运动，设加速度大小分别为$a_{1}$和$a_{2}$，
得$a_{1} = \frac{\mu mg}{m} = \mu g = 2\ m/s^{2}$，$a_{2} = \frac{\mu mg}{M} = 4\ m/s^{2}$
根据运动学规律，对游客$v = v_{0} - a_{1}t$
解得$t = 1\ s$
该段时间内游客的位移为$x_{1} = \frac{v + v_{0}}{2}t = 9\ m$
滑板的位移为$x_{2} = \frac{1}{2}a_{2}t^{2} = 2\ m$
根据位移关系得滑板的长度为$L = x_{1} - x_{2} = 7\ m$