《2025年步步高大一轮复习讲义物理教科版》

9. (2025·江苏省扬州大学附属中学开学考)我国某新型潜航器在某次试航中，测试垂直急速下潜、上浮性能，水面舰艇上的测试员发现仪表上显示潜航器在某时刻的速度为正值，加速度也是正值且加速度大小不断减小直到为零，则该潜航器的运动情况为(C)

A.位移先增大后减小，直到加速度等于零为止
B.位移一直在增大，直到加速度等于零为止
C.速度一直在增大，直到加速度等于零为止
D.速度先增大后减小，直到加速度等于零为止

答案： 9.C　[由于加速度的方向始终与速度方向相同，则速度一直在增大，当加速度减小到零时，速度达到最大值，故C正确，D错误;位移一直在增大，当加速度减小到零时，速度不再变化，但位移随时间继续增大，故A、B错误。]

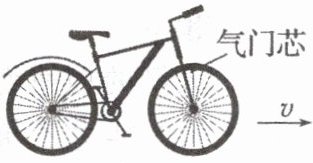
10. (2024·山东滨州市期末)如图，自行车在水平地面上做匀速直线运动。车轮外边缘半径为$R$，气门芯距轮心的距离为$r$，自行车行驶过程中轮胎不打滑，初始时刻气门芯在最高点，不考虑车轮的形变。气门芯从初始时刻到第一次运动至最低点过程中位移的大小为(D)

A.$\sqrt{4R^2+\pi^2R^2}$
B.$\sqrt{4R^2+\pi^2r^2}$
C.$\sqrt{4r^2+\pi^2r^2}$
D.$\sqrt{4r^2+\pi^2R^2}$

答案：
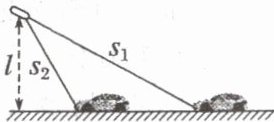
10.D　[当气门芯由轮子的正上方 第一次运动到轮子的正下方时，轮子向前运动半个周长，气门芯的初位置与末位置如图所示，由几何知识得，气门芯的位移大小为$x = \sqrt{(2r)^2 + (\pi R)^2} = \sqrt{4r^2 + \pi^2 R^2}$，故D正确。]

11. (2024·四川德阳市诊断)激光测速仪能够测量运动物体的瞬时速率，其测量精度较高，广泛应用于交通管理等领域。如图所示，测速仪向汽车发射一束激光，经反射后被接收装置接收。只要测出从发射到接收所经历的时间，便可得到测速仪到汽车的距离。在测量时，测速仪在较短时间$\Delta t = 0.1s$内分别发射两束激光，对汽车进行两次这样的距离测量，其中$s_1 = 10m$，$s_2 = 7.5m$，已知测速仪高$l = 6m$，则汽车的速度大小为(C)

A.$80m/s$
B.$45m/s$
C.$35m/s$
D.$25m/s$

答案： 11.C　[由题图中几何关系可知，在$\Delta t$时间内，汽车前进的位移为$x = \sqrt{s_1^2 - l^2} - \sqrt{s_2^2 - l^2} = \sqrt{10^2 - 6^2}m - \sqrt{7.5^2 - 6^2}m = 3.5m$，因为$\Delta t$很小，故汽车的速度可认为等于$\Delta t$时间内的平均速度，则有$v = \frac{x}{\Delta t} = \frac{3.5}{0.1}m/s = 35m/s$，故C正确。]

12. (2024·浙江温州市模拟)一列队伍长$120m$，正以某一速度做匀速直线运动，因有紧急情况需要通知排头兵，一名通讯员以不变的速率从队尾跑至排头，又从排头赶至队尾，在此过程中队伍前进了$288m$，则通讯员在该过程中往返的路程是(D)

A.$576m$
B.$216\sqrt{2}m$
C.$408m$
D.$432m$

答案： 12.D　[设通讯员的速度大小为$v_1$，队伍的速度大小为$v_2$，通讯员从队尾到排头的时间为$t_1$，从排头到队尾的时间为$t_2$，队伍前进所用时间为$t$。由通讯员往返总时间与队伍运动时间相等可得$t = t_1 + t_2$，即$\frac{288m}{v_2} = \frac{120m}{v_1 - v_2} + \frac{120m}{v_1 + v_2}$，解得$v_1 = \frac{3}{2}v_2$，则$s_1 = v_1t = \frac{3}{2}v_2t = \frac{3}{2} × 288m = 432m$，故选D。]

13. (16分)(2025·湖南邵阳市检测)如图所示，一固定的超声波测速仪每隔$1s$向小汽车发出一个超声波脉冲信号，已知第一个超声波$t_0 = 0$时刻发出，遇到小汽车后返回，$t_1 = 1.3s$时刻测速仪接收到第一个反射波，$t_2 = 2.4s$时刻接收到第二个反射波。若超声波在空气中的传播速度为$340m/s$，小汽车在这段时间的运动视为匀速直线运动，根据上述条件，求：
(1)(8分)小汽车第一、第二次接触超声波时分别与测速仪间的距离；
(2)(8分)小汽车在前两次接触超声波期间的平均速度大小(结果保留三位有效数字)。

答案： 13.
(1)221m　238m　
(2)16.2m/s
解析　
(1)第一次超声波接触小汽车时超声波测速仪与小汽车之间的距离为$x_1 = v \cdot \frac{t_1}{2} = \frac{340 × 1.3}{2}m = 221m$
第二次超声波接触小汽车时超声波测速仪与小汽车之间的距离为$x_2 = v \cdot \frac{t_2 - \Delta t}{2} = 340 × \frac{2.4 - 1}{2}m = 238m$
(2)小汽车前进的位移$x = x_2 - x_1 = (238 - 221)m = 17m$
经过的时间为$t = \Delta t + \frac{t_2 - \Delta t}{2} - \frac{t_1}{2} = (1 + \frac{2.4 - 1}{2} - \frac{1.3}{2})s = 1.05s$
小汽车的平均速度为$\overline{v} = \frac{x}{t} = \frac{17}{1.05}m/s \approx 16.2m/s$。