《2025年步步高大一轮复习讲义物理教科版》

8. (多选)(2021·河北卷·9)如图，矩形金属框MNQP竖直放置，其中MN、PQ足够长，且PQ杆光滑，一根轻弹簧一端固定在M点，另一端连接一个质量为m的小球，小球穿过PQ杆，金属框绕MN轴分别以角速度$\omega$和$\omega'$匀速转动时，小球均相对PQ杆静止，若$\omega' ＞ \omega$，则与以$\omega$匀速转动时相比，以$\omega'$匀速转动时(BD)


A.小球的高度一定降低
B.弹簧弹力的大小一定不变
C.小球对杆压力的大小一定变大
D.小球所受合外力的大小一定变大

答案： 8.BD [对小球受力分析，设弹簧弹力为$F_{T}$，弹簧与水平方向的夹角为$\theta$，则对小球竖直方向有$F_{T}\sin\theta = mg$，而$F_{T}=k(\frac{MP}{\cos\theta}-l_{0})$，可知$\theta$为定值，$F_{T}$不变，则当转速增大后，小球的高度不变，弹簧的弹力不变，A错误，B正确；水平方向当转速较小，杆对小球的弹力背离转轴时，则$F_{T}\cos\theta - F_{N}=m\omega^{2}r$，即$F_{N}=F_{T}\cos\theta - m\omega^{2}r$；当转速较大，杆对小球的弹力指向转轴时，则$F_{T}\cos\theta + F_{N}' = m\omega'^{2}r$，即$F_{N}' = m\omega'^{2}r - F_{T}\cos\theta$，因$\omega'＞\omega$，根据牛顿第三定律可知，小球对杆的压力不一定变大，C错误；根据$F_{合}=m\omega^{2}r$可知，因角速度变大，则小球所受合外力变大，D正确。]

9. (16分)(八省联考·陕西·14)图(a)是某小河的航拍照片，河道弯曲形成的主要原因之一可解释为：河道弯曲处的内侧与外侧河堤均受到流水重力产生的压强，外侧河堤还受到流水冲击产生的压强。小河某弯道处可视为半径为R的圆弧的一部分，如图(b)所示，假设河床水平，河水密度为$\rho$，河道在整个弯道处宽度d和水深h均保持不变，水的流动速度v大小恒定，$d \ll R$，忽略流水内部的相互作用力。取弯道某处一垂直于流速的观测截面，求在一极短时间$\Delta t$内：(R、$\rho$、d、h、v、$\Delta t$均为已知量)

(1)(5分)通过观测截面的流水质量$\Delta m$；
(2)(5分)流水速度改变量$\Delta v$的大小；
(3)(6分)外侧河堤受到的流水冲击产生的压强p。

答案： 9.
(1)$\rho dhv\cdot\Delta t$
(2)$\frac{v^{2}}{R}\cdot\Delta t$
(3)$\frac{\rho dv^{2}}{R}$ 解析
(1)由题可知，极短时间$\Delta t$内水流的长度$\Delta l = v\cdot\Delta t$，由于横截面积为$S = dh$，根据$\rho=\frac{m}{V}$，可得水的质量$\Delta m=\rho\cdot\Delta V=\rho dhv\cdot\Delta t$；
(2)由于$\Delta t$极短，可以把水的运动简化为匀速圆周运动，根据匀速圆周运动的规律可知，其加速度为$a=\frac{v^{2}}{R}$，又因为$a=\frac{\Delta v}{\Delta t}$，联立解得$\Delta v=\frac{v^{2}}{R}\cdot\Delta t$；
(3)根据牛顿第二定律可得$F = \Delta m\cdot\frac{v^{2}}{R}$，联立上述结论，解得$F=\frac{\rho dhv^{3}\cdot\Delta t}{R}$，水流与河堤作用的面积$S'=\Delta l\cdot h = vh\cdot\Delta t$，故外侧河堤受到的流水冲击产生的压强$p=\frac{F}{S'}=\frac{\frac{\rho dhv^{3}\cdot\Delta t}{R}}{vh\cdot\Delta t}=\frac{\rho dv^{2}}{R}$。

10. (18分)(2024·江西卷·14)雪地转椅是一种游乐项目，其中心传动装置带动转椅在雪地上滑动。如图(a)、(b)所示，传动装置有一高度可调的水平圆盘，可绕通过中心O点的竖直轴匀速转动。圆盘边缘A处固定连接一轻绳，轻绳另一端B连接转椅(视为质点)。转椅运动稳定后，其角速度与圆盘角速度相等。转椅与雪地之间的动摩擦因数为$\mu$，重力加速度为g，不计空气阻力。

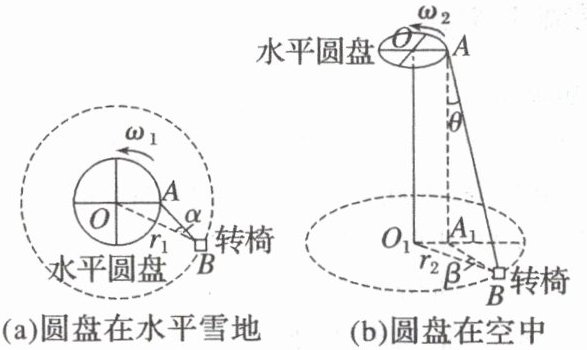
(1)(9分)在图(a)中，若圆盘在水平雪地上以角速度$\omega_1$匀速转动，转椅运动稳定后在水平雪地上绕O点做半径为$r_1$的匀速圆周运动。求AB与OB之间夹角$\alpha$的正切值。
(2)(9分)将圆盘升高，如图(b)所示。圆盘匀速转动，转椅运动稳定后在水平雪地上绕$O_1$点做半径为$r_2$的匀速圆周运动，绳子与竖直方向的夹角为$\theta$，绳子在水平雪地上的投影$A_1B$与$O_1B$的夹角为$\beta$。求此时圆盘的角速度$\omega_2$。

答案： 10.
(1)$\frac{\mu g}{\omega_{1}^{2}r_{1}}$
(2)$\sqrt{\frac{\mu g\sin\theta\cos\beta}{(\sin\theta\sin\beta+\mu\cos\theta)r_{2}}}$ 解析
(1)设转椅做匀速圆周运动时轻绳拉力为$F_{T}$，转椅质量为$m$，受力分析可知轻绳拉力沿切线方向的分量与转椅受到地面的滑动摩擦力平衡，沿径向方向的分量提供转椅做圆周运动的向心力，故可得$F_{T}\cos\alpha = m\omega_{1}^{2}r_{1}$，$\mu mg = F_{T}\sin\alpha$，联立解得$\tan\alpha=\frac{\mu g}{\omega_{1}^{2}r_{1}}$；
(2)设此时轻绳拉力为$F_{T}'$，沿$A_{1}B$方向和垂直$A_{1}B$方向竖直向上的分力分别为$F_{T1}=F_{T}'\sin\theta$，$F_{T2}=F_{T}'\cos\theta$，对转椅根据牛顿第二定律得$F_{T1}\cos\beta=m\omega_{2}^{2}r_{2}$，沿切线方向根据平衡条件有$F_{T1}\sin\beta=F_{1}=\mu F_{N}$，竖直方向根据平衡条件有$F_{N}+F_{T2}=mg$，联立解得$\omega_{2}=\sqrt{\frac{\mu g\sin\theta\cos\beta}{(\sin\theta\sin\beta+\mu\cos\theta)r_{2}}}$。