《2025年步步高大一轮复习讲义物理教科版》

8. (2024·山东卷·5)“鹊桥二号”中继星环绕月球运行，其 24 小时椭圆轨道的半长轴为 $a$。已知地球同步卫星的轨道半径为 $r$，则月球与地球质量之比可表示为(D)

A.$\sqrt{\frac{r^{3}}{a^{3}}}$
B.$\sqrt{\frac{a^{3}}{r^{3}}}$
C.$\frac{r^{3}}{a^{3}}$
D.$\frac{a^{3}}{r^{3}}$

答案： 8.D [由$\frac{GMm}{r^{2}}=m\frac{4\pi^{2}}{T^{2}}r$得：$\frac{r^{3}}{T^{2}}=\frac{GM}{4\pi^{2}}$根据开普勒第三定律$\frac{r^{3}}{T^{2}}=k，$则$k=\frac{GM}{4\pi^{2}}$可见，开普勒第三定律中的k值与中心天体质量有关，地球质量$M_{地}=\frac{4\pi^{2}r^{3}}{GT^{2}}，$同理，对“鹊桥二号”中继星，可得月球质量$M_{月}=\frac{4\pi^{2}a^{3}}{GT_{月}^{2}}，$因“鹊桥二号”与地球同步卫星周期相同，所以$\frac{M_{月}}{M_{地}}=\frac{a^{3}}{r^{3}}，$故选D。]

9. (2025·重庆市松树桥中学月考)如图所示，$A$、$B$ 两颗卫星绕地球做匀速圆周运动，$O$ 为地心，在两卫星运行过程中，$AB$ 连线和 $OA$ 连线的夹角最大为 $\theta$，则 $A$、$B$ 两卫星(C)

A.做圆周运动的周期之比为 $2\sqrt{\frac{1}{\sin^{3}\theta}}$
B.做圆周运动的周期之比为 $\frac{1}{\sin^{3}\theta}$
C.与地心 $O$ 连线在相等时间内扫过的面积之比为 $\sqrt{\frac{1}{\sin\theta}}$
D.与地心 $O$ 连线在相等时间内扫过的面积之比为 $\frac{1}{\sin\theta}$

答案： 9.C [夹角最大时，OB与AB垂直，根据几何关系有$r_{B}=r_{A}\sin\theta，$由开普勒第三定律可得$\frac{T_{A}^{2}}{T_{B}^{2}}=\frac{r_{A}^{3}}{r_{B}^{3}}，$则$\frac{T_{A}}{T_{B}}=\sqrt{\frac{1}{\sin^{3}\theta}}，$A、B错误；t时间内，卫星与地心连线扫过的面积$S=\frac{t}{T} \cdot \pi r^{2}，$则$\frac{S_{A}}{S_{B}}=\frac{T_{B}}{T_{A}} \cdot \frac{r_{A}^{2}}{r_{B}^{2}}=\sqrt{\frac{1}{\sin\theta}}，$C正确，D错误。]

10. 将一质量为 $m$ 的物体分别放在地球的南、北两极点时，该物体的重力均为 $mg_{0}$；将该物体放在地球赤道上时，该物体的重力为 $mg$。假设地球可视为质量均匀分布的球体，半径为 $R$，已知引力常量为 $G$，则由以上信息可得出(C)

A.$g_{0}$ 小于 $g$
B.地球的质量为 $\frac{gR^{2}}{G}$
C.地球自转的角速度为 $\omega=\sqrt{\frac{g_{0} - g}{R}}$
D.地球的平均密度为 $\frac{3g}{4\pi GR}$

答案： 10.C [设地球的质量为M，物体在赤道处随地球自转做圆周运动的角速度等于地球自转的角速度，轨道半径等于地球半径，物体在赤道上受到的重力和物体随地球自转所需的向心力是万有引力的分力，有$G\frac{Mm}{R^{2}}-mg=m\omega^{2}R，$物体在两极受到的重力等于万有引力，即$G\frac{Mm}{R^{2}}=mg_{0}，$所以$g_{0}＞g，$故A错误；在两极有$mg_{0}=G\frac{Mm}{R^{2}}，$解得$M=\frac{g_{0}R^{2}}{G}，$故B错误；由$G\frac{Mm}{R^{2}}-mg=m\omega^{2}R，$$mg_{0}=G\frac{Mm}{R^{2}}，$解得$\omega=\sqrt{\frac{g_{0}-g}{R}}，$故C正确；地球的平均密度$\rho=\frac{M}{V}=\frac{\frac{g_{0}R^{2}}{G}}{\frac{4}{3}\pi R^{3}}=\frac{3g_{0}}{4\pi GR}，$故D错误。]

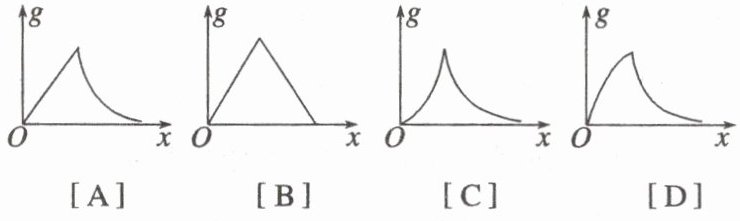
11. (2024·贵州省六校联盟模拟)已知质量分布均匀的球壳对内部物体产生的万有引力为 0。对于某质量分布均匀的星球，在距离星球表面不同高度或不同深度处重力加速度大小是不同的，若用 $x$ 表示某位置到该星球球心的距离，用 $g$ 表示该位置处的重力加速度大小，忽略星球自转，下列关于 $g$ 与 $x$ 的关系图像可能正确的是(A)


A.
B.
C.
D.

答案： 11.A [设星球的半径为R，地球的密度为$\rho，$当$x\leq R，$距地球球心x处的物体受到的万有引力与该处的重力的关系为$G\frac{\frac{4}{3}\pi x^{3}\rho m}{x^{2}}=mg，$可得$g=\frac{4\pi G\rho x}{3}，$当x＞R，距地球球心x处的物体受到的万有引力与该处的重力的关系为$G\frac{\frac{4}{3}\pi R^{3}\rho m}{x^{2}}=mg，$可得$g=\frac{4\pi G\rho R^{3}}{3x^{2}}，$故选A。]