2025年步步高大一轮复习讲义物理教科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年步步高大一轮复习讲义物理教科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第314页
- 第307页
- 第308页
- 第309页
- 第310页
- 第311页
- 第312页
- 第313页
- 第314页
- 第315页
- 第316页
- 第317页
- 第318页
- 第319页
- 第320页
- 第321页
- 第322页
- 第323页
- 第324页
- 第325页
- 第326页
- 第327页
- 第328页
- 第329页
- 第330页
- 第331页
- 第332页
- 第333页
- 第334页
- 第335页
- 第336页
- 第337页
- 第338页
- 第339页
- 第340页
- 第341页
- 第342页
- 第343页
- 第344页
- 第345页
- 第346页
- 第347页
- 第348页
- 第349页
- 第350页
- 第351页
- 第352页
- 第353页
- 第354页
- 第355页
- 第356页
- 第357页
- 第358页
- 第359页
- 第360页
- 第361页
- 第362页
- 第363页
- 第364页
- 第365页
- 第366页
- 第367页
- 第368页
- 第369页
- 第370页
- 第371页
- 第372页
- 第373页
- 第374页
- 第375页
- 第376页
- 第377页
- 第378页
- 第379页
- 第380页
- 第381页
- 第382页
- 第383页
- 第384页
- 第385页
- 第386页
- 第387页
- 第388页
- 第389页
- 第390页
- 第391页
- 第392页
- 第393页
- 第394页
- 第395页
- 第396页
- 第397页
- 第398页
- 第399页
- 第400页
- 第401页
- 第402页
- 第403页
- 第404页
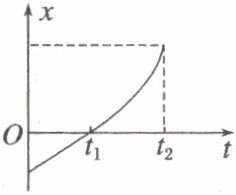
6. 一质点运动的位移—时间图像如图所示,其中 $ 0 \sim t_1 $ 为直线,$ t_1 \sim t_2 $ 为抛物线,则有关质点运动的速度—时间图像及加速度—时间图像可能正确的是(
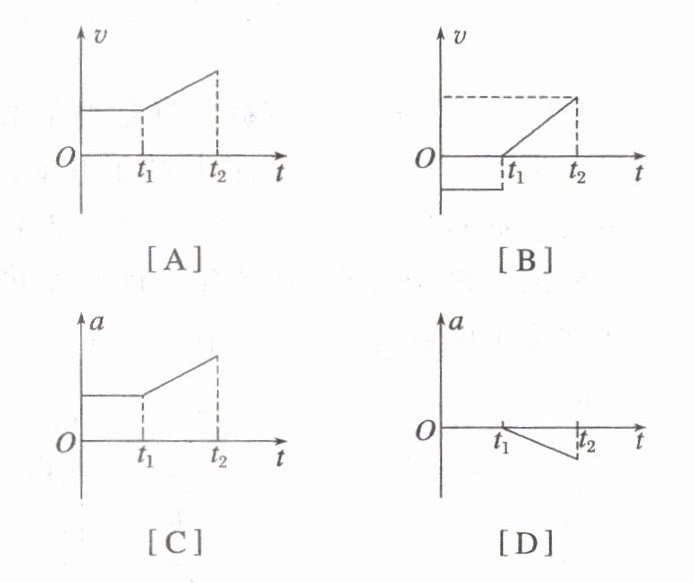
A
)

答案:
6.A [位移—时间图像中,$0~t_{1}$为直线,则质点做匀速直线运动,$t_{1}~t_{2}$为抛物线,则质点做匀加速直线运动,故A正确。]
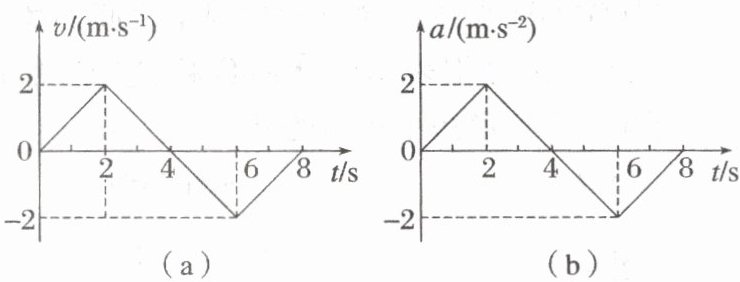
7. (多选)(2023·福建卷·7 改编)甲、乙两辆完全相同的小车均由静止沿同一方向出发做直线运动。以出发时刻为计时零点,甲车的速度—时间图像如图(a)所示,乙车的加速度—时间图像如图(b)所示。则(
A.$ 0 \sim 2 \, s $ 内,甲车的加速度大小逐渐增大
B.乙车在 $ t = 2 \, s $ 和 $ t = 6 \, s $ 时的速度相同
C.$ 2 \sim 6 \, s $ 内,甲、乙两车的位移不同
D.$ t = 8 \, s $ 时,甲、乙两车的速度不同
BC
)
A.$ 0 \sim 2 \, s $ 内,甲车的加速度大小逐渐增大
B.乙车在 $ t = 2 \, s $ 和 $ t = 6 \, s $ 时的速度相同
C.$ 2 \sim 6 \, s $ 内,甲、乙两车的位移不同
D.$ t = 8 \, s $ 时,甲、乙两车的速度不同
答案:
7.BC [由题图(a)可知$0~2s$内,甲车做匀加速直线运动,加速度大小不变,故A错误;由题图(b)可知乙车在$0~2s$内的速度变化量等于$a-t$图像与$t$轴围成的面积,故$t = 2s$时的速度为$2m/s$,同理可知乙车在$t = 6s$时的速度为$2m/s$,故B正确;根据题图(a)可知,$2~6s$内甲车的位移为$0$;根据题图(b)可知,$2~6s$内乙车一直向正方向运动,则$2~6s$内,甲、乙两车的位移不同,故C正确;根据题图(a)可知,$t = 8s$时甲车的速度为$0$,由题图(b)可知,乙车在$0~8s$内速度变化量为$0$,故$t = 8s$时乙车的速度为$0$,故D错误。]
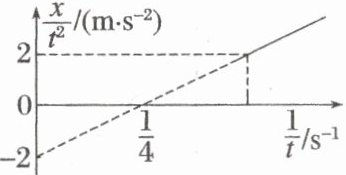
8. (2024·贵州贵阳市检测)无人配送小车在某次进行刹车性能测试时,其位移 $ x $ 与时间 $ t $ 的关系可用如图所示的图像表示,则下列说法正确的是(
A.前 $ 4 \, s $ 小车做匀加速直线运动
B.前 $ 3 \, s $ 内小车的位移大小为 $ 8 \, m $
C.小车运动的初速度大小为 $ 4 \, m/s $
D.小车运动的加速度大小为 $ 2 \, m/s^2 $
B
)
A.前 $ 4 \, s $ 小车做匀加速直线运动
B.前 $ 3 \, s $ 内小车的位移大小为 $ 8 \, m $
C.小车运动的初速度大小为 $ 4 \, m/s $
D.小车运动的加速度大小为 $ 2 \, m/s^2 $
答案:
8.B [根据匀变速直线运动位移时间关系式$x = v_{0}t + \frac{1}{2}at^{2}$,得$\frac{x}{t^{2}} = \frac{v_{0}}{t} + \frac{1}{2}a$,则$\frac{x}{t^{2}}-\frac{1}{t}$图像是一条倾斜的直线,由题图可知,图线斜率为小车运动的初速度,则$v_{0} = \frac{0 - (-2)}{\frac{1}{4}}m/s = 8m/s$,纵截距为小车运动的加速度的$\frac{1}{2}$,则$\frac{1}{2}a = -2m/s^{2}$,则$a = -4m/s^{2}$,小车刹车时间为$t = \frac{-v_{0}}{a} = 2s$,故前$3s$内小车的位移即前$2s$内的位移,大小为$x = \frac{v_{0}}{2}t = 8m$,前$2s$小车做匀减速直线运动,$2s$后停止。故选B。]
9. (2024·山东烟台市三模)在非洲的干旱草原和半沙漠地带有一种猫科动物狞猫,狞猫跳跃能力极强,奔跑速度快,能捉降落或起飞时的鸟类。某次狞猫在捕食树上的鸟时,先慢慢趴低身体,使身体贴近地面,然后突然蹬地向上加速,重心上升后离地向上运动,狞猫在离开地面前,其加速度 $ a $ 与重心上升高度 $ h $ 的关系如图所示,忽略空气阻力,重力加速度 $ g $ 取 $ 10 \, m/s^2 $,则狞猫离地后重心上升的最大高度为(
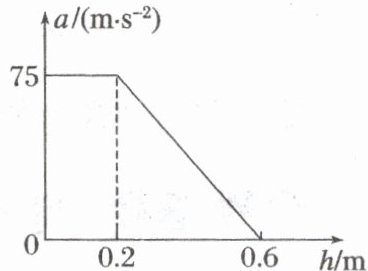
A.$ 1.5 \, m $
B.$ 3 \, m $
C.$ 4.5 \, m $
D.$ 6 \, m $
B
)
A.$ 1.5 \, m $
B.$ 3 \, m $
C.$ 4.5 \, m $
D.$ 6 \, m $
答案:
9.B [根据题意,设狞猫离地时速度为$v$,根据动力学公式$v^{2} = 2ah$,整理得$\frac{v^{2}}{2} = ah$,可知$a-h$图像与$h$轴围成的面积表示$\frac{v^{2}}{2}$,则$\frac{v^{2}}{2} = (75 × 0.2 + \frac{1}{2} × 75 × 0.4)m^{2}/s^{2}$,解得$v = 2\sqrt{15}m/s$,狞猫离地后,根据动力学公式$v^{2} = 2gh'$,解得狞猫离地后重心上升的最大高度为$h' = 3m$,故选B。]
10. (2024·湖北武汉市模拟)甲、乙两物体沿 $ x $ 轴正方向做直线运动,某一时刻两物体以速度 $ v_0 $ 同时经过 $ O $ 点,之后它们运动的 $ \frac{1}{v} - x $ 图像如图所示,则甲、乙两物体速度从 $ v_0 $ 增加到 $ 2v_0 $ 的过程,下列说法中正确的是(
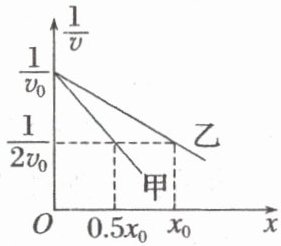
A.速度均随位移均匀变化
B.速度均随时间均匀变化
C.经历的时间之比为 $ 1 : 2 $
D.经历的时间之比为 $ 2 : 1 $
C
)
A.速度均随位移均匀变化
B.速度均随时间均匀变化
C.经历的时间之比为 $ 1 : 2 $
D.经历的时间之比为 $ 2 : 1 $
答案:
10.C [由题图可知,$\frac{1}{v}$与$x$成线性关系,则$v$与$x$不成线性关系,即速度不随位移均匀变化,故A错误;$\frac{1}{v}-x$图像的图线与$x$轴围成的面积表示时间,则$\frac{x}{v} = t$,$v$与$x$不成线性关系,则速度不随时间均匀变化,故B错误;$\frac{1}{v}-x$图像的图线与$x$轴围成的面积表示时间,则甲、乙两物体速度从$v_{0}$增加到$2v_{0}$的过程,经历的时间之比为$1:2$,故C正确,D错误。]
11. (多选)如图所示为某质点做直线运动的 $ v - t $ 图像,其中 $ Oa $、$ ab $ 是关于 $ a $ 点的中心对称图形。下列说法正确的是(
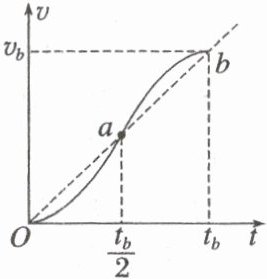
A.$ 0 \sim \frac{t_b}{2} $ 内,质点速度增量为 $ \frac{v_b}{2} $
B.$ 0 \sim t_b $ 内,质点运动的位移为 $ \frac{1}{2}v_b t_b $
C.$ \frac{t_b}{4} $、$ \frac{3t_b}{4} $ 两时刻,质点的加速度不相等
D.$ \frac{t_b}{2} \sim t_b $ 内,质点运动的位移是 $ \frac{3v_b t_b}{8} $
AB
)
A.$ 0 \sim \frac{t_b}{2} $ 内,质点速度增量为 $ \frac{v_b}{2} $
B.$ 0 \sim t_b $ 内,质点运动的位移为 $ \frac{1}{2}v_b t_b $
C.$ \frac{t_b}{4} $、$ \frac{3t_b}{4} $ 两时刻,质点的加速度不相等
D.$ \frac{t_b}{2} \sim t_b $ 内,质点运动的位移是 $ \frac{3v_b t_b}{8} $
答案:
11.AB [根据图像的中心对称可知,$a$点的坐标是$(\frac{t_{b}}{2},\frac{v_{b}}{2})$,则$0~\frac{t_{b}}{2}$内质点速度增量$\Delta v = v_{a} - 0 = \frac{v_{b}}{2}$,A正确;$v-t$图像中图线与$t$轴所围的面积表示质点在该段时间内发生的位移,$0~t_{b}$时间内,在$v-t$图像上进行割补,其面积恰好等于三角形$Obt_{b}$的面积,所以质点运动的位移等于$\frac{1}{2}v_{b}t_{b}$,B正确;$v-t$图像中图线的斜率表示质点的加速度,根据图像的中心对称可知,$\frac{t_{b}}{4}$、$\frac{3t_{b}}{4}$这两时刻的图像斜率相等,加速度相等,C错误;若质点做加速度为$\frac{v_{b}}{t_{b}}$的匀加速直线运动,质点的$v-t$图像为题图中的斜虚线,在$\frac{t_{b}}{2}~t_{b}$时间内质点的位移为图中阴影部分面积,可得$x_{匀加速} = (\frac{v_{b}}{2} + v_{b}) × \frac{t_{b}}{2} × \frac{1}{2} = \frac{3v_{b}t_{b}}{8}$,由图可知在$\frac{t_{b}}{2}~t_{b}$时间内质点的$v-t$图像与$t$轴所围面积大于图中阴影部分面积,故在$\frac{t_{b}}{2}~t_{b}$时间内质点的位移大于$\frac{3v_{b}t_{b}}{8}$,D错误。 ]
]
11.AB [根据图像的中心对称可知,$a$点的坐标是$(\frac{t_{b}}{2},\frac{v_{b}}{2})$,则$0~\frac{t_{b}}{2}$内质点速度增量$\Delta v = v_{a} - 0 = \frac{v_{b}}{2}$,A正确;$v-t$图像中图线与$t$轴所围的面积表示质点在该段时间内发生的位移,$0~t_{b}$时间内,在$v-t$图像上进行割补,其面积恰好等于三角形$Obt_{b}$的面积,所以质点运动的位移等于$\frac{1}{2}v_{b}t_{b}$,B正确;$v-t$图像中图线的斜率表示质点的加速度,根据图像的中心对称可知,$\frac{t_{b}}{4}$、$\frac{3t_{b}}{4}$这两时刻的图像斜率相等,加速度相等,C错误;若质点做加速度为$\frac{v_{b}}{t_{b}}$的匀加速直线运动,质点的$v-t$图像为题图中的斜虚线,在$\frac{t_{b}}{2}~t_{b}$时间内质点的位移为图中阴影部分面积,可得$x_{匀加速} = (\frac{v_{b}}{2} + v_{b}) × \frac{t_{b}}{2} × \frac{1}{2} = \frac{3v_{b}t_{b}}{8}$,由图可知在$\frac{t_{b}}{2}~t_{b}$时间内质点的$v-t$图像与$t$轴所围面积大于图中阴影部分面积,故在$\frac{t_{b}}{2}~t_{b}$时间内质点的位移大于$\frac{3v_{b}t_{b}}{8}$,D错误。
 ]
] 查看更多完整答案,请扫码查看


