2025年步步高大一轮复习讲义物理教科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年步步高大一轮复习讲义物理教科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第310页
- 第307页
- 第308页
- 第309页
- 第310页
- 第311页
- 第312页
- 第313页
- 第314页
- 第315页
- 第316页
- 第317页
- 第318页
- 第319页
- 第320页
- 第321页
- 第322页
- 第323页
- 第324页
- 第325页
- 第326页
- 第327页
- 第328页
- 第329页
- 第330页
- 第331页
- 第332页
- 第333页
- 第334页
- 第335页
- 第336页
- 第337页
- 第338页
- 第339页
- 第340页
- 第341页
- 第342页
- 第343页
- 第344页
- 第345页
- 第346页
- 第347页
- 第348页
- 第349页
- 第350页
- 第351页
- 第352页
- 第353页
- 第354页
- 第355页
- 第356页
- 第357页
- 第358页
- 第359页
- 第360页
- 第361页
- 第362页
- 第363页
- 第364页
- 第365页
- 第366页
- 第367页
- 第368页
- 第369页
- 第370页
- 第371页
- 第372页
- 第373页
- 第374页
- 第375页
- 第376页
- 第377页
- 第378页
- 第379页
- 第380页
- 第381页
- 第382页
- 第383页
- 第384页
- 第385页
- 第386页
- 第387页
- 第388页
- 第389页
- 第390页
- 第391页
- 第392页
- 第393页
- 第394页
- 第395页
- 第396页
- 第397页
- 第398页
- 第399页
- 第400页
- 第401页
- 第402页
- 第403页
- 第404页
9. (2023·山东卷·6)如图所示,电动公交车做匀减速直线运动进站,连续经过 $R$、$S$、$T$ 三点,已知 $ST$ 间的距离是 $RS$ 的两倍,$RS$ 段的平均速度是 10 m/s,$ST$ 段的平均速度是 5 m/s,则公交车经过 $T$ 点时的瞬时速度为(
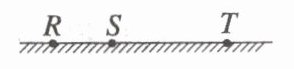
A.$3 \, m/s$
B.$2 \, m/s$
C.$1 \, m/s$
D.$0.5 \, m/s$
C
)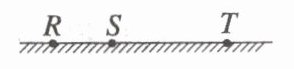
A.$3 \, m/s$
B.$2 \, m/s$
C.$1 \, m/s$
D.$0.5 \, m/s$
答案:
9.C 由题知,电动公交车做匀减速直线运动,设RS间的距离为$x$,则根据题意有$\overline{v}_{RS} = \frac{x}{t_1} = \frac{v_R + v_S}{2}$,$\overline{v}_{ST} = \frac{2x}{t_2} = \frac{v_S + v_T}{2}$
联立解得$t_2 = 4t_1$,$v_T = v_R - 10$,
再根据匀变速直线运动速度与时间的关系有$v_T = v_R - a \cdot 5t_1$,则$at_1 = 2 m/s$,
又有$\overline{v}_{RS} = v_R - a \cdot \frac{t_1}{2} = 10 m/s$,则$v_R = 11 m/s$,
联立解得$v_T = 1 m/s$,故选C。
联立解得$t_2 = 4t_1$,$v_T = v_R - 10$,
再根据匀变速直线运动速度与时间的关系有$v_T = v_R - a \cdot 5t_1$,则$at_1 = 2 m/s$,
又有$\overline{v}_{RS} = v_R - a \cdot \frac{t_1}{2} = 10 m/s$,则$v_R = 11 m/s$,
联立解得$v_T = 1 m/s$,故选C。
10. (15 分)(2024·广西卷·13)如图,轮滑训练场沿直线等间距地摆放着若干个定位锥筒,锥筒间距 $d = 0.9 \, m$,某同学穿着轮滑鞋向右匀减速滑行。现测出他从 1 号锥筒运动到 2 号锥筒用时 $t_1 = 0.4 \, s$,从 2 号锥筒运动到 3 号锥筒用时 $t_2 = 0.5 \, s$。求该同学

(1) (7 分)滑行的加速度大小;
(2) (8 分)最远能经过几号锥筒。

(1) (7 分)滑行的加速度大小;
(2) (8 分)最远能经过几号锥筒。
答案:
10.
(1)$1 m/s^2$
(2)4
解析
(1)根据匀变速直线运动规律,某段内的平均速度等于中间时刻的瞬时速度,可知在1、2间中间时刻的速度为$v_1 = \frac{d}{t_1} = 2.25 m/s$
2、3间中间时刻的速度为
$v_2 = \frac{d}{t_2} = 1.8 m/s$
故可得加速度大小为
$a = \frac{\Delta v}{\Delta t} = \frac{v_1 - v_2}{\frac{t_1}{2} + \frac{t_2}{2}} = 1 m/s^2$
(2)设到达1号锥筒时的速度为$v_0$,根据匀变速直线运动规律得$v_1 = v_0 - a \cdot \frac{t_1}{2}$
代入数据解得$v_0 = 2.45 m/s$
从1号开始到停止时通过的位移大小为$x = \frac{v_0^2}{2a} = 3.00125 m \approx 3.33d$
故可知最远能经过4号锥筒。
(1)$1 m/s^2$
(2)4
解析
(1)根据匀变速直线运动规律,某段内的平均速度等于中间时刻的瞬时速度,可知在1、2间中间时刻的速度为$v_1 = \frac{d}{t_1} = 2.25 m/s$
2、3间中间时刻的速度为
$v_2 = \frac{d}{t_2} = 1.8 m/s$
故可得加速度大小为
$a = \frac{\Delta v}{\Delta t} = \frac{v_1 - v_2}{\frac{t_1}{2} + \frac{t_2}{2}} = 1 m/s^2$
(2)设到达1号锥筒时的速度为$v_0$,根据匀变速直线运动规律得$v_1 = v_0 - a \cdot \frac{t_1}{2}$
代入数据解得$v_0 = 2.45 m/s$
从1号开始到停止时通过的位移大小为$x = \frac{v_0^2}{2a} = 3.00125 m \approx 3.33d$
故可知最远能经过4号锥筒。
11. (2025·天津市耀华中学期中)一质点做匀变速直线运动,已知初速度大小为 $v$,经过一段时间速度大小为 $2v$,加速度大小为 $a$,这段时间内的路程与位移之比为 $5 : 3$,则下列说法正确的是(
A.这段时间内质点运动方向不变
B.这段时间为 $\frac{3v}{a}$
C.这段时间质点运动的路程为 $\frac{3v^2}{2a}$
D.再经过相同时间,质点速度大小为 $3v$
B
)A.这段时间内质点运动方向不变
B.这段时间为 $\frac{3v}{a}$
C.这段时间质点运动的路程为 $\frac{3v^2}{2a}$
D.再经过相同时间,质点速度大小为 $3v$
答案:
11.B 由题意知,质点先做匀减速直线运动,速度减小到零后,再反向做匀加速直线运动,即在这段时间内运动方向改变,如图所示,选项A错误;由$v = v_0 + at$得$-2v = v - at$,可得时间$t = \frac{3v}{a}$,选项B正确;由$v^2 - v_0^2 = 2ax$得,从初速度为$v$减速到零所通过的路程$x_1 = \frac{v^2}{2a}$,然后反向加速到$2v$所通过的路程$x_2 = \frac{(2v)^2}{2a} = \frac{2v^2}{a}$,总路程为$x = x_1 + x_2 = \frac{5v^2}{2a}$,选项C错误;再经过相同时间,质点速度为$v' = v - a \cdot 2t = -5v$,即速度大小为$5v$,选项D错误。
查看更多完整答案,请扫码查看


