2025年步步高大一轮复习讲义物理教科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年步步高大一轮复习讲义物理教科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第357页
- 第307页
- 第308页
- 第309页
- 第310页
- 第311页
- 第312页
- 第313页
- 第314页
- 第315页
- 第316页
- 第317页
- 第318页
- 第319页
- 第320页
- 第321页
- 第322页
- 第323页
- 第324页
- 第325页
- 第326页
- 第327页
- 第328页
- 第329页
- 第330页
- 第331页
- 第332页
- 第333页
- 第334页
- 第335页
- 第336页
- 第337页
- 第338页
- 第339页
- 第340页
- 第341页
- 第342页
- 第343页
- 第344页
- 第345页
- 第346页
- 第347页
- 第348页
- 第349页
- 第350页
- 第351页
- 第352页
- 第353页
- 第354页
- 第355页
- 第356页
- 第357页
- 第358页
- 第359页
- 第360页
- 第361页
- 第362页
- 第363页
- 第364页
- 第365页
- 第366页
- 第367页
- 第368页
- 第369页
- 第370页
- 第371页
- 第372页
- 第373页
- 第374页
- 第375页
- 第376页
- 第377页
- 第378页
- 第379页
- 第380页
- 第381页
- 第382页
- 第383页
- 第384页
- 第385页
- 第386页
- 第387页
- 第388页
- 第389页
- 第390页
- 第391页
- 第392页
- 第393页
- 第394页
- 第395页
- 第396页
- 第397页
- 第398页
- 第399页
- 第400页
- 第401页
- 第402页
- 第403页
- 第404页
1. (多选)关于地球同步卫星,下列说法正确的是(
A.它的周期与地球自转周期相同
B.它的周期、高度、速度大小都是一定的
C.它的速度大小随高度的变化而变化,但周期都是一定的
D.我国发射的同步通信卫星可以定点在北京上空
AB
)A.它的周期与地球自转周期相同
B.它的周期、高度、速度大小都是一定的
C.它的速度大小随高度的变化而变化,但周期都是一定的
D.我国发射的同步通信卫星可以定点在北京上空
答案:
1.AB
2. (八省联考·云南·2)神舟十九号载人飞船与中国空间站完成自主交会对接后形成一个组合体。该组合体在距地面高约 400 km(高于近地轨道高度)的轨道上运行,其轨道可近似视为圆。已知地球同步卫星位于地面上方高度约 36 000 km 处,则该组合体(
A.运行速度大于 7.9 km/s,运行周期小于地球同步卫星的周期
B.运行速度大于 7.9 km/s,运行周期大于地球同步卫星的周期
C.运行速度小于 7.9 km/s,运行周期小于地球同步卫星的周期
D.运行速度小于 7.9 km/s,运行周期大于地球同步卫星的周期
C
)A.运行速度大于 7.9 km/s,运行周期小于地球同步卫星的周期
B.运行速度大于 7.9 km/s,运行周期大于地球同步卫星的周期
C.运行速度小于 7.9 km/s,运行周期小于地球同步卫星的周期
D.运行速度小于 7.9 km/s,运行周期大于地球同步卫星的周期
答案:
2.C 根据$G\frac{Mm}{r^{2}} = m\frac{v^{2}}{r} = m\frac{4\pi^{2}}{T^{2}}r$可得$v = \sqrt{\frac{GM}{r}}$,$T = 2\pi\sqrt{\frac{r^{3}}{GM}}$组合体的轨道半径大于近地卫星轨道半径,可知组合体的运行速度小于$7.9km/s$;组合体轨道半径小于同步卫星的轨道半径,可知组合体的运行周期小于地球同步卫星的周期,故选C。
3. (2024·山东滨州市期末)2023 年 12 月 15 日,我国在文昌航天发射场使用长征五号遥六运载火箭成功将遥感四十一号卫星发射升空,卫星顺利进入预定轨道,发射任务获得圆满成功。某遥感卫星沿地球同步轨道运行,关于该遥感卫星,下列说法正确的是(
A.其运行速度等于 7.9 km/s
B.其向心加速度大于放在赤道上的物体的向心加速度
C.其向心加速度大于地球表面的重力加速度
D.已知该卫星的轨道半径和地球自转的周期,不能求出该卫星的线速度大小
B
)A.其运行速度等于 7.9 km/s
B.其向心加速度大于放在赤道上的物体的向心加速度
C.其向心加速度大于地球表面的重力加速度
D.已知该卫星的轨道半径和地球自转的周期,不能求出该卫星的线速度大小
答案:
3.B 卫星所受的万有引力提供做匀速圆周运动的向心力,即$G\frac{Mm}{r^{2}} = m\frac{v^{2}}{r}$,解得$v = \sqrt{\frac{GM}{r}}$,因为$7.9km/s$是近地卫星的环绕速度,且近地卫星的环绕半径比地球同步卫星小,则该遥感卫星的线速度小于近地卫星的线速度,即其运行速度小于$7.9km/s$,故A错误;因为该卫星与赤道上的物体环绕周期和角速度相等,该卫星的环绕半径大于赤道上的物体随地球做匀速圆周运动的半径,根据$a = \omega^{2}r$可知,其向心加速度大于放在赤道上的物体的向心加速度,故B正确;根据$G\frac{Mm}{r^{2}} = ma$,解得该卫星的向心加速度$a = \frac{GM}{r^{2}}$,设地球半径为$R$,地球表面的重力加速度为$g$,有$G\frac{Mm}{R^{2}} = mg$,解得$g = \frac{GM}{R^{2}}$,因为$r > R$,则$a < g$,故C错误;地球自转的周期与该卫星做匀速圆周运动的周期相等,该卫星的轨道半径和环绕周期都已知,根据$v = \frac{2\pi r}{T}$可知,能求出该卫星的线速度大小,故D错误。
4. (九省联考·贵州·2)天宫空间站运行过程中因稀薄气体阻力的影响,每经过一段时间要进行轨道修正,使其回到原轨道。修正前、后天宫空间站的运动均可视为匀速圆周运动,则与修正前相比,修正后天宫空间站运行的(
A.轨道半径减小
B.速率减小
C.向心加速度增大
D.周期减小
B
)A.轨道半径减小
B.速率减小
C.向心加速度增大
D.周期减小
答案:
4.B 天宫空间站运行过程中因稀薄气体阻力的影响,天宫空间站的机械能减小,天宫空间站轨道高度降低,则与修正前相比,修正后天宫空间站运行的轨道半径增大,故A错误;根据万有引力提供向心力$G\frac{Mm}{r^{2}} = m\frac{v^{2}}{r} = m\frac{4\pi^{2}}{T^{2}}r = ma$可得$v = \sqrt{\frac{GM}{r}}$,$T = 2\pi\sqrt{\frac{r^{3}}{GM}}$,$a = \frac{GM}{r^{2}}$,修正后天宫空间站运行的轨道半径增大,则速率和向心加速度均减小,周期增大,故B正确,C、D错误。
5. (2025·陕西西安市调研)如图所示,a 为放在赤道上相对地球静止的物体,随地球自转做匀速圆周运动,b 为沿地球表面附近做匀速圆周运动的人造卫星(轨道半径约等于地球半径),c 为地球的静止轨道卫星。下列关于 a、b、c 的说法中正确的是(
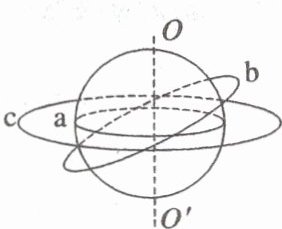
A.地球同步卫星都与 c 在同一个轨道上,并且它们受到的万有引力大小相等
B.a、b、c 做匀速圆周运动的向心加速度大小关系为 $ a_{a} > a_{b} > a_{c} $
C.a 与地球的万有引力全部提供 a 随地球自转的向心力
D.a、b、c 做匀速圆周运动的周期大小关系为 $ T_{a} = T_{c} > T_{b} $
D
)
A.地球同步卫星都与 c 在同一个轨道上,并且它们受到的万有引力大小相等
B.a、b、c 做匀速圆周运动的向心加速度大小关系为 $ a_{a} > a_{b} > a_{c} $
C.a 与地球的万有引力全部提供 a 随地球自转的向心力
D.a、b、c 做匀速圆周运动的周期大小关系为 $ T_{a} = T_{c} > T_{b} $
答案:
5.D 地球同步卫星一定与$c$在同一轨道上,但轨道半径相等,卫星的质量不一定相等,由万有引力定律$F = G\frac{Mm}{r^{2}}$可知,它们受到的万有引力大小不一定相等,A错误;对于$b$、$c$,由万有引力提供向心力有$G\frac{Mm}{r^{2}} = ma$,解得$a = \frac{GM}{r^{2}}$,$r_{c} > r_{b}$,所以$a_{b} > a_{c}$,由于$a$、$c$做匀速圆周运动的周期相等,又$a = r\omega^{2}$,$\omega = \frac{2\pi}{T}$,$r_{c} > r_{a}$,可得$a_{c} > a_{a}$,所以$a$、$b$、$c$做匀速圆周运动的向心加速度大小关系为$a_{b} > a_{c} > a_{a}$,B错误;$a$与地球的万有引力一部分提供$a$随地球自转的向心力,C错误;对于$a$、$c$,其周期相等,所以$T_{a} = T_{c}$,对于$b$、$c$,由万有引力提供向心力有$G\frac{Mm}{r^{2}} = mr\frac{4\pi^{2}}{T^{2}}$,解得$T = 2\pi\sqrt{\frac{r^{3}}{GM}}$,$r_{c} > r_{b}$,所以$T_{c} > T_{b}$,即$a$、$b$、$c$做匀速圆周运动的周期大小关系为$T_{a} = T_{c} > T_{b}$,D正确。
6. (2024·江西卷·4)“嫦娥六号”探测器于 2024 年 5 月 8 日进入环月轨道,后续经调整环月轨道高度和倾角,实施月球背面软着陆。当探测器的轨道半径从 $ r_{1} $ 调整到 $ r_{2} $ 时(两轨道均可视为圆形轨道),其动能和周期从 $ E_{k1} $、$ T_{1} $ 分别变为 $ E_{k2} $、$ T_{2} $。下列选项正确的是(
A.$ \dfrac{E_{k1}}{E_{k2}} = \dfrac{r_{2}}{r_{1}} $,$ \dfrac{T_{1}}{T_{2}} = \dfrac{\sqrt{r_{1}^{3}}}{\sqrt{r_{2}^{3}}} $
B.$ \dfrac{E_{k1}}{E_{k2}} = \dfrac{r_{1}}{r_{2}} $,$ \dfrac{T_{1}}{T_{2}} = \dfrac{\sqrt{r_{1}^{3}}}{\sqrt{r_{2}^{3}}} $
C.$ \dfrac{E_{k1}}{E_{k2}} = \dfrac{r_{2}}{r_{1}} $,$ \dfrac{T_{1}}{T_{2}} = \dfrac{\sqrt{r_{2}^{3}}}{\sqrt{r_{1}^{3}}} $
D.$ \dfrac{E_{k1}}{E_{k2}} = \dfrac{r_{1}}{r_{2}} $,$ \dfrac{T_{1}}{T_{2}} = \dfrac{\sqrt{r_{2}^{3}}}{\sqrt{r_{1}^{3}}} $
A
)A.$ \dfrac{E_{k1}}{E_{k2}} = \dfrac{r_{2}}{r_{1}} $,$ \dfrac{T_{1}}{T_{2}} = \dfrac{\sqrt{r_{1}^{3}}}{\sqrt{r_{2}^{3}}} $
B.$ \dfrac{E_{k1}}{E_{k2}} = \dfrac{r_{1}}{r_{2}} $,$ \dfrac{T_{1}}{T_{2}} = \dfrac{\sqrt{r_{1}^{3}}}{\sqrt{r_{2}^{3}}} $
C.$ \dfrac{E_{k1}}{E_{k2}} = \dfrac{r_{2}}{r_{1}} $,$ \dfrac{T_{1}}{T_{2}} = \dfrac{\sqrt{r_{2}^{3}}}{\sqrt{r_{1}^{3}}} $
D.$ \dfrac{E_{k1}}{E_{k2}} = \dfrac{r_{1}}{r_{2}} $,$ \dfrac{T_{1}}{T_{2}} = \dfrac{\sqrt{r_{2}^{3}}}{\sqrt{r_{1}^{3}}} $
答案:
6.A 探测器在环月轨道做匀速圆周运动,则月球对探测器的万有引力提供向心力,设月球的质量为$M$,探测器的质量为$m$,则半径为$r_{1}$时有$G\frac{Mm}{r_{1}^{2}} = m\frac{v_{1}^{2}}{r_{1}}$,半径为$r_{2}$时有$G\frac{Mm}{r_{2}^{2}} = m\frac{v_{2}^{2}}{r_{2}} = m\frac{4\pi^{2}}{T_{2}^{2}}r_{2}$,再根据动能$E_{k} = \frac{1}{2}mv^{2}$,可得调整前后动能和周期的比值分别为$\frac{E_{k1}}{E_{k2}} = \frac{r_{2}}{r_{1}}$,$\frac{T_{1}}{T_{2}} = \sqrt{\frac{r_{1}^{3}}{r_{2}^{3}}}$故选A。
查看更多完整答案,请扫码查看


