《2025年作业本江西教育出版社八年级数学上册北师大版》

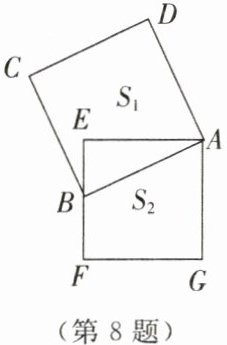
8. 如图，$ S_1 $ 和 $ S_2 $ 分别为正方形 $ ABCD $ 和正方形 $ AEFG $ 的面积，点 $ B $ 在 $ EF $ 上，$ S_1 = 140 $，$ S_2 = 124 $，$ EB $ 的长为4。

答案： 4
解：
∵$ S_1 = 140 ，$$ S_2 = 124 ，$
∴ 正方形 ABCD 的边长$ AB = \sqrt{140} ，$正方形 AEFG 的边长$ AE = \sqrt{124} 。$
设 EB = x ， BF = y ，
∵ 四边形 AEFG 是正方形，
∴$ \angle AEB = 90° ，$$ EF = AE = \sqrt{124} ，$
∴$ \angle AEB = 90° ，$
在$ Rt\triangle AEB $中，由勾股定理得：
$ AE^2 + EB^2 = AB^2 ，$
即$ (\sqrt{124})^2 + x^2 = (\sqrt{140})^2 ，$
$ 124 + x^2 = 140 ，$
$ x^2 = 16 ，$
x = 4 （负值舍去），
∴ EB = 4 。
答案：4

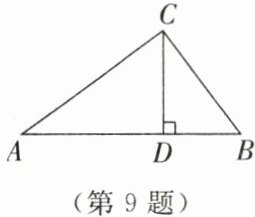
9. 如图，在 $ \triangle ABC $ 中，$ CD \perp AB $ 于点 $ D $，$ AC = 4 $，$ BC = 3 $，$ AD = \dfrac{16}{5} $。
（1）求 $ CD $，$ BD $ 的长。
（2）判断 $ \triangle ABC $ 的形状，并说明理由。

答案： 解：​
(1)​在​ Rt△ACD ​中
$​CD^2=AC^2-AD^2=4^2-(\frac {16}5)^2=(\frac {12}5)^2​$
∴$​CD=\frac {12}5​$
在​ Rt △BCD ​中
$​BD^2=BC^2-CD^2=3^2-(\frac {12}5)^2=(\frac 95)^2​$
∴$​BD=\frac 95​$
​
(2)△ ABC ​为直角三角形，理由如下：
$​AB=AD+BD=\frac {16}5+\frac 95=5​$
∵$​3^2+4^2=5^2​$
即$​ BC^2+AC^2=AB^2​$
∴​△ABC ​为直角三角形

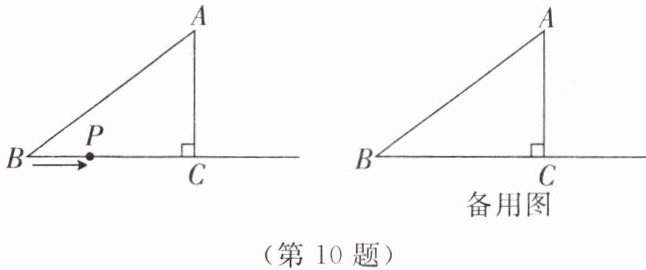
10. 如图，在 $ Rt \triangle ABC $ 中，$ \angle ACB = 90^{\circ} $，$ AB = 10 cm $，$ AC = 6 cm $。动点 $ P $ 从点 $ B $ 出发沿射线 $ BC $ 以 $ 2 cm/s $ 的速度运动，设运动时间为 $ t s $。
（1）求 $ BC $ 的长。
（2）当 $ \triangle ABP $ 为直角三角形时，求 $ t $ 的值。

答案： 解：​
(1)​在​ Rt △ABC ​中，
$​BC^2=AB^2-AC^2=10^2-6^2=64​$
∴​BC=8 ​
​
(2)​由题意可知，$​BP=2\ \mathrm {t}​$
分两种情况讨论：
​①​当​ ∠AP B ​为直角时，点​ P ​与点​ C ​重合
​BP=BC=8，​即​ t=4​
​②​当​ ∠BAP ​为直角时，
$​BP=2\ \mathrm {t}，$​​CP=(2t-8)，​​AC=6​
在​ Rt△ACP ​中，$​AP^2=6^2+(2\ \mathrm {t}-8)^2​$
在​ Rt △BAP ​中，$​AB^2+AP^2=BP^2​$
∴$​10^2+6^2+(2t-8)^2=(2t)^2​$
解得$​ t=\frac {25}4​$
∴当​△ ABP ​为直角三角形时，
​t=4 ​或$​ \frac {25}4​$