《2025年作业本江西教育出版社八年级数学上册北师大版》

1. 下图是小岩、小轩、小颖做课间操时的位置，老师建立了一个平面直角坐标系。如果用坐标 $ (3,5) $ 表示小岩的位置，坐标 $ (2,3) $ 表示小轩的位置，那么小颖的位置用坐标表示为(B)

A.$ (4,3) $
B.$ (4,2) $
C.$ (-4,2) $
D.$ (0,2) $
]

答案： B
解：由小岩(3,5)、小轩(2,3)的坐标，确定平面直角坐标系：以小岩所在列向右为x轴正方向，所在行向上为y轴正方向，每个小方格边长为1个单位长度，坐标原点在小岩左3列、下5行处。
小颖在小轩右2列、下1行，小轩坐标(2,3)，则小颖横坐标为2+2=4，纵坐标为3-1=2，坐标为(4,2)。
答案：B

2. 如图，长方形 $ ABCD $ 的边 $ CD $ 在 $ y $ 轴上， $ O $ 为 $ CD $ 的中点。若 $ AB = 4 $， $ AB $ 交 $ x $ 轴于点 $ E(-5,0) $，则点 $ B $ 的坐标为(D)

A.$ (-5,2) $
B.$ (2,5) $
C.$ (5,-2) $
D.$ (-5,-2) $
]

答案： D
解：
∵四边形ABCD是长方形，
∴AB=CD=4，AB//CD，AD=BC，AD//BC。
∵CD在y轴上，O为CD中点，
∴O为坐标原点(0,0)，CO=OD=2。
∵AB交x轴于点E(-5,0)，AB//CD（y轴），
∴AB⊥x轴，点B与点E横坐标相同，为-5。
∵BC//x轴，点C在y轴上且OC=2，点C在x轴下方，
∴点C坐标为(0,-2)，点B纵坐标与点C相同，为-2。
∴点B坐标为(-5,-2)。
答案：D

3. 如图，四边形 $ ABCD $ 是边长为 4 的正方形，在正方形的一个角上剪去长方形 $ CEFG $，其中 $ E $， $ G $ 分别是边 $ CD $， $ BC $ 上的点，且 $ CE = 3 $， $ CG = 2 $，剩余部分是六边形 $ ABGFED $。请你建立适当的平面直角坐标系，并写出六边形 $ ABGFED $ 各顶点的坐标。

答案：

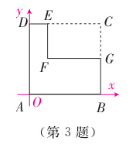
解：以点A为原点，AB所在直线为x轴，AD所在直线为y轴，建立平面直角坐标系。
因为四边形ABCD是边长为4的正方形，
所以A(0,0)，B(4,0)，C(4,4)，D(0,4)。
因为CE=3，CG=2，
所以E点坐标为(4-3,4)=(1,4)，G点坐标为(4,4-2)=(4,2)。
因为CEFG是长方形，
所以F点坐标为(1,2)。
综上，六边形ABGFED各顶点的坐标分别为：A(0,0)，B(4,0)，G(4,2)，F(1,2)，E(1,4)，D(0,4)。
解：如图所示
A(0，0)，B(4，0)，G(4，2)，F(1，2)，
E(1，4)，D(0，4)

4. 如图，在以点 $ O $ 为原点的平面直角坐标系中，点 $ A $， $ B $ 的坐标分别为 $ (a,0) $， $ (a,b) $，点 $ C $ 在 $ y $ 轴上，且 $ BC // x $ 轴， $ a $， $ b $ 满足 $ |a - 3|+\sqrt{b - 4}=0 $。点 $ P $ 从原点出发，以每秒 2 个单位长度的速度沿着 $ OA \to AB \to BC \to CO $ 的路线运动，回到点 $ O $ 时运动停止。
（1）直接写出点 $ A $， $ B $， $ C $ 的坐标。
（2）当点 $ P $ 运动 3 s 时，求出点 $ P $ 的坐标。
（3）点 $ P $ 运动 $ t(t \neq 0) $ s 后，是否存在点 $ P $ 到 $ x $ 轴的距离为 $ \frac{1}{2}t $ 个单位长度的情况？若存在，直接写出点 $ P $ 的坐标；若不存在，请说明理由。
]

答案： 解：​
(1)A(3，​​0)，​​B(3，​​4)，​​C(0，​​4)​
​
(2)​当点​P ​运动$​3\ \mathrm {s} ​$时，点​P ​运动了​6​个单位长度
∵​AO=3，​​AB=4​
∴点​P ​运动$​3\ \mathrm {s} ​$时，
点​P ​在线段​AB​上，且​AP=3​
∴点​P ​的坐标是​(3，​​3)​
​
(3)​存在
点​P ​的坐标为​(3，​​1)​或​(0，$​​\frac {14}5)​$