第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 小明用火柴棒摆直角三角形,他摆两条直角边分别用了 6 根和 8 根火柴棒,摆完这个直角三角形共用火柴棒(
A.20 根
B.14 根
C.24 根
D.30 根
C
)A.20 根
B.14 根
C.24 根
D.30 根
答案:
C
解:因为直角三角形两条直角边分别用了6根和8根火柴棒,根据勾股定理,斜边的火柴棒数量为:$\sqrt{6^{2}+8^{2}}=\sqrt{36 + 64}=\sqrt{100}=10($根)。则摆完这个直角三角形共用火柴棒:6 + 8 + 10 = 24(根)。
C
解:因为直角三角形两条直角边分别用了6根和8根火柴棒,根据勾股定理,斜边的火柴棒数量为:$\sqrt{6^{2}+8^{2}}=\sqrt{36 + 64}=\sqrt{100}=10($根)。则摆完这个直角三角形共用火柴棒:6 + 8 + 10 = 24(根)。
C
2. 如图,四个全等的直角三角形和中间的小正方形可以拼成一个大正方形。若直角三角形较长的直角边的长度为 a,较短的直角边的长度为 b,大正方形的面积为 S₁,小正方形的面积为 S₂,则(a + b)² 可以表示为(
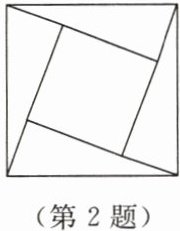
A.S₁ - S₂
B.S₁ + S₂
C.2S₁ - S₂
D.S₁ + 2S₂
C
)
A.S₁ - S₂
B.S₁ + S₂
C.2S₁ - S₂
D.S₁ + 2S₂
答案:
C
解:
由题意,大正方形边长为直角三角形斜边,设为 c ,则$ S_1 = c^2 。$
小正方形边长为 a - b ,则$ S_2 = (a - b)^2 = a^2 - 2ab + b^2 。$
因直角三角形全等,$ 4 × \frac{1}{2}ab + S_2 = S_1 ,$即$ 2ab = S_1 - S_2 。$
又$ a^2 + b^2 = c^2 = S_1 ,$
则$ (a + b)^2 = a^2 + 2ab + b^2 = S_1 + (S_1 - S_2) = 2S_1 - S_2 。$
答案:C
解:
由题意,大正方形边长为直角三角形斜边,设为 c ,则$ S_1 = c^2 。$
小正方形边长为 a - b ,则$ S_2 = (a - b)^2 = a^2 - 2ab + b^2 。$
因直角三角形全等,$ 4 × \frac{1}{2}ab + S_2 = S_1 ,$即$ 2ab = S_1 - S_2 。$
又$ a^2 + b^2 = c^2 = S_1 ,$
则$ (a + b)^2 = a^2 + 2ab + b^2 = S_1 + (S_1 - S_2) = 2S_1 - S_2 。$
答案:C
3. 我国古代著名的“赵爽弦图”是由四个全等的直角三角形围成的正方形,如图所示。如果 AE = 5,AB = 13,那么 EF² =(
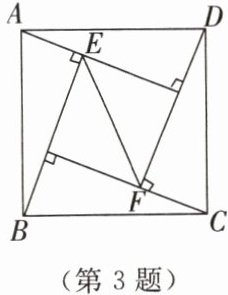
A.49
B.12
C.13
D.98
D
)
A.49
B.12
C.13
D.98
答案:
D
4. 如图,若将一根长 12 cm 的筷子置于底面直径为 6 cm、高为 8 cm 的圆柱形杯子中,则筷子露在杯子外面的长度 h 至少为
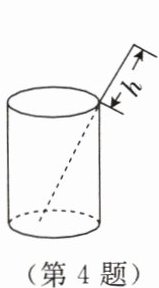
2
cm。
答案:
【解析】:
本题可先根据圆柱的底面直径和高,利用勾股定理求出筷子在杯子中的最大长度,再用筷子的总长度减去在杯子中的最大长度,即可得到筷子露在杯子外面的最小长度。
步骤一:分析筷子在杯子中的最大长度
将筷子置于圆柱形杯子中,筷子在杯子中的最大长度就是杯子内部对角线的长度。
此时杯子内部可看作一个底面直径为6cm、高为8cm的长方体(将圆柱的底面直径看作长方体的底面长,圆柱的高看作长方体的高),筷子在杯子中的最大长度就是这个长方体的对角线长度。
根据勾股定理,若直角三角形的两条直角边长度分别为a和b,斜边长度为c,则$a^2 + b^2 = c^2。$
在由杯子底面直径、高和杯子内部对角线构成的直角三角形中,底面直径的一半(6÷2 = 3cm)和高8cm为两条直角边,杯子内部对角线为斜边。
设杯子内部对角线长度为l,则$l=\sqrt{6^{2}+8^{2}}。$
计算$\sqrt{6^{2}+8^{2}}=\sqrt{36 + 64}=\sqrt{100}=10cm,$即筷子在杯子中的最大长度为10cm。
步骤二:计算筷子露在杯子外面的最小长度
已知筷子的总长度为12cm,由步骤一可知筷子在杯子中的最大长度为10cm,那么筷子露在杯子外面的最小长度h = 12 - 10 = 2cm。
【答案】:2
本题可先根据圆柱的底面直径和高,利用勾股定理求出筷子在杯子中的最大长度,再用筷子的总长度减去在杯子中的最大长度,即可得到筷子露在杯子外面的最小长度。
步骤一:分析筷子在杯子中的最大长度
将筷子置于圆柱形杯子中,筷子在杯子中的最大长度就是杯子内部对角线的长度。
此时杯子内部可看作一个底面直径为6cm、高为8cm的长方体(将圆柱的底面直径看作长方体的底面长,圆柱的高看作长方体的高),筷子在杯子中的最大长度就是这个长方体的对角线长度。
根据勾股定理,若直角三角形的两条直角边长度分别为a和b,斜边长度为c,则$a^2 + b^2 = c^2。$
在由杯子底面直径、高和杯子内部对角线构成的直角三角形中,底面直径的一半(6÷2 = 3cm)和高8cm为两条直角边,杯子内部对角线为斜边。
设杯子内部对角线长度为l,则$l=\sqrt{6^{2}+8^{2}}。$
计算$\sqrt{6^{2}+8^{2}}=\sqrt{36 + 64}=\sqrt{100}=10cm,$即筷子在杯子中的最大长度为10cm。
步骤二:计算筷子露在杯子外面的最小长度
已知筷子的总长度为12cm,由步骤一可知筷子在杯子中的最大长度为10cm,那么筷子露在杯子外面的最小长度h = 12 - 10 = 2cm。
【答案】:2
5. 在学习了勾股定理后,同学们了解到该定理有多种证法。某同学提出了一种利用图形拼接的验证思路:如图①,B 是正方形 ACDE 的边 CD 上的一点,连接 AB,得到直角三角形 ACB(其三条边的长度分别为 a,b,c);将△ACB 剪下并拼接至△AEF 的位置,如图②所示。该同学通过分析图①和图②的面积关系验证了勾股定理。请你根据上述思路进行验证。
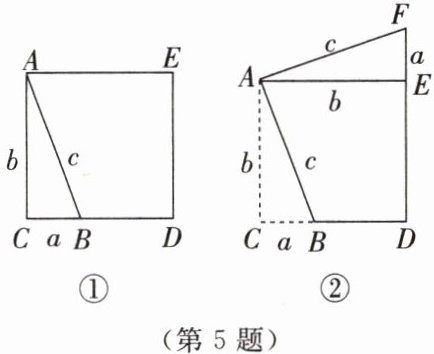

答案:

解:如图②,连接BF
由题意可知△ACB≌△ AEF
∴AB=AF
∴△BAF 是等腰直角三角形
∴$S_{四边形ABDF}=S_{△BAF}+S_{△F BD}$
$=\frac 12\ \mathrm {A}B·AF+\frac 12BD·DF$
$=\frac 12c^2+\frac 12(b-a)(b+a)$
$=\frac 12c^2+\frac 12(b^2-a^2)$
∵$S_{四边形ACDE}=b^2,$
$S_{四边形ACDE}=S_{四边形ABDF}$
∴$b^2=\frac 12c^2+\frac 12(b^2-a^2)$
化简,得$a^2+b^2=c^2$

解:如图②,连接BF
由题意可知△ACB≌△ AEF
∴AB=AF
∴△BAF 是等腰直角三角形
∴$S_{四边形ABDF}=S_{△BAF}+S_{△F BD}$
$=\frac 12\ \mathrm {A}B·AF+\frac 12BD·DF$
$=\frac 12c^2+\frac 12(b-a)(b+a)$
$=\frac 12c^2+\frac 12(b^2-a^2)$
∵$S_{四边形ACDE}=b^2,$
$S_{四边形ACDE}=S_{四边形ABDF}$
∴$b^2=\frac 12c^2+\frac 12(b^2-a^2)$
化简,得$a^2+b^2=c^2$
查看更多完整答案,请扫码查看


