第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
20. 【探究发现】
(1)如图①,在等边三角形 ABC 中,P 为三角形内一点,连接 AP,BP,CP。当 $ \angle APB - \angle ABC = 90^{\circ} $ 时,AP,BP,CP 满足 $ AP^{2} + BP^{2} = CP^{2} $。数学兴趣小组的同学们通过讨论,得到了以下思路:以 AP 为边,在 AP 的左侧作等边三角形 APQ,连接 BQ,通过验证 $ \triangle APC \cong \triangle AQB $,从而得到 $ PC = BQ $;再通过验证 $ \triangle PBQ $ 是直角三角形,得到 $ QP^{2} + BP^{2} = QB^{2} $,经等量代换即可得到 AP,BP,CP 的关系。请你根据以上思路,完成推导过程。
【类比】
(2)如图②,$ \triangle ABC $ 是等腰直角三角形,$ AB = AC $,P 为三角形内一点,连接 AP,BP,CP。当 $ \angle APB - \angle ABC = 90^{\circ} $ 时,判断 AP,BP,CP 之间的数量关系,并说明理由。
【联想拓展】
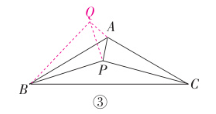
(3)如图③,在等腰三角形 ABC 中,$ AB = AC $,$ \angle BAC = 120^{\circ} $,P 为三角形内一点,连接 AP,BP,CP。当 $ \angle APB - \angle ABC = 90^{\circ} $ 时,AP,BP,CP 满足 $ (kAP)^{2} + BP^{2} = CP^{2} $,请直接写出 k 的值。


(1)如图①,在等边三角形 ABC 中,P 为三角形内一点,连接 AP,BP,CP。当 $ \angle APB - \angle ABC = 90^{\circ} $ 时,AP,BP,CP 满足 $ AP^{2} + BP^{2} = CP^{2} $。数学兴趣小组的同学们通过讨论,得到了以下思路:以 AP 为边,在 AP 的左侧作等边三角形 APQ,连接 BQ,通过验证 $ \triangle APC \cong \triangle AQB $,从而得到 $ PC = BQ $;再通过验证 $ \triangle PBQ $ 是直角三角形,得到 $ QP^{2} + BP^{2} = QB^{2} $,经等量代换即可得到 AP,BP,CP 的关系。请你根据以上思路,完成推导过程。
【类比】
(2)如图②,$ \triangle ABC $ 是等腰直角三角形,$ AB = AC $,P 为三角形内一点,连接 AP,BP,CP。当 $ \angle APB - \angle ABC = 90^{\circ} $ 时,判断 AP,BP,CP 之间的数量关系,并说明理由。
【联想拓展】
(3)如图③,在等腰三角形 ABC 中,$ AB = AC $,$ \angle BAC = 120^{\circ} $,P 为三角形内一点,连接 AP,BP,CP。当 $ \angle APB - \angle ABC = 90^{\circ} $ 时,AP,BP,CP 满足 $ (kAP)^{2} + BP^{2} = CP^{2} $,请直接写出 k 的值。


答案:
∴$AB = AC,$$AQ = AP = PQ,$
∴$∠BAC - ∠BAP = ∠Q AP - ∠BAP$
∴$∆P AC≌∆Q AB,$
∴$P C = Q B$
∵$∠AP B - ∠ABC = 90°$
∴$∠AP B - ∠APQ = 90°,$即$∠QP B = 90°$
∴$QP^2+BP^2=Q B^2$
∵$AP = QP,$$BQ = CP$
∴$AP^2+BP^2=CP^2$
∵$∆ABC$和$∆AQP $是等腰直角三角形
∴$AB = AC,$$AQ = AP,$$∠BAC = ∠Q AP = 90°,$
∴$∠BAC - ∠BAP = ∠Q AP - ∠BAP,$
∴$∆P AC≌∆Q AB,$
∴$P C = Q B$
∵$∠AP B - ∠ABC = 90°$
∴$∠AP B - ∠APQ = 90°,$即$∠QP B = 90°$
∴$QP^2+BP^2=Q B^2$
∵$∆AQP $是等腰直角三角形
∴$AP^2+AQ^2=QP^2$
∵$AP = AQ,$
∴$QP^2=2\ \mathrm {AP}^2$
∴$2\ \mathrm {AP}^2+BP^2=CP^2$

解:$(1)$
∵$∆ABC$和$∆AQP $是等边三角形
∵$∆ABC$和$∆AQP $是等边三角形
∴$AB = AC,$$AQ = AP = PQ,$
$∠BAC = ∠ABC = ∠APQ = ∠Q AP = 60°$
∴$∠BAC - ∠BAP = ∠Q AP - ∠BAP$
即$∠P AC = ∠Q AB$
∴$∆P AC≌∆Q AB,$
∴$P C = Q B$
∵$∠AP B - ∠ABC = 90°$
∴$∠AP B - ∠APQ = 90°,$即$∠QP B = 90°$
∴$QP^2+BP^2=Q B^2$
∵$AP = QP,$$BQ = CP$
∴$AP^2+BP^2=CP^2$
$(2)$如图$②,$以$AP $为边,在$AP $的左侧作
等腰直角三角形$APQ,$使得$AP = AQ,$连接$BQ$
∵$∆ABC$和$∆AQP $是等腰直角三角形
∴$AB = AC,$$AQ = AP,$$∠BAC = ∠Q AP = 90°,$
$∠ABC = ∠APQ = 45°$
∴$∠BAC - ∠BAP = ∠Q AP - ∠BAP,$
即$∠P AC = ∠Q AB$
∴$∆P AC≌∆Q AB,$
∴$P C = Q B$
∵$∠AP B - ∠ABC = 90°$
∴$∠AP B - ∠APQ = 90°,$即$∠QP B = 90°$
∴$QP^2+BP^2=Q B^2$
∵$∆AQP $是等腰直角三角形
∴$AP^2+AQ^2=QP^2$
∵$AP = AQ,$
∴$QP^2=2\ \mathrm {AP}^2$
∴$2\ \mathrm {AP}^2+BP^2=CP^2$
$(3)$辅助线如图所示,$k=\sqrt 3$
查看更多完整答案,请扫码查看


