《2025年作业本江西教育出版社八年级数学上册北师大版》

1. 下列关于有序数对的说法正确的是(C)

A.$(3,2)$与$(2,3)$表示的位置相同
B.$(a,b)$与$(b,a)$表示的位置相同
C.$(5,6)$与$(6,5)$是表示不同位置的两个有序数对
D.$(4,4)$与$(4,4)$表示两个不同的位置

答案： C
【解析】：
本题主要考察有序数对的概念。有序数对(a,b)中，a代表第一个元素，b代表第二个元素，两者不能互换，即(a,b)与(b,a)表示的位置不同，除非a=b。
A. 对于(3,2)与(2,3)，由于$3 \neq 2，$所以它们表示的位置不同，故A选项错误；
B. 对于(a,b)与(b,a)，除非a=b，否则它们表示的位置不同，故B选项错误；
C. 对于(5,6)与(6,5)，由于$5 \neq 6，$所以它们表示的位置不同，故C选项正确；
D. 对于(4,4)与(4,4)，它们完全相同，所以表示的位置相同，故D选项错误。
【答案】：C

2. $\triangle AOB$关于$x$轴对称的图形是$\triangle A'OB$。若$\triangle AOB$内任意一点$P$的坐标是$(a,b)$，则点$P$在$\triangle A'OB$内的对应点$Q$的坐标是(D)

A.$(a,b)$
B.$(-a,b)$
C.$(-a,-b)$
D.$(a,-b)$

答案： D
解：关于x轴对称的点，横坐标相同，纵坐标互为相反数。
∵点P(a,b)在△AOB内，△AOB与△A'OB关于x轴对称，
∴点P的对应点Q的坐标是(a,-b)。
答案：D

3. 已知$a + b＞0$，$ab＞0$。在如图所示的平面直角坐标系中，小手盖住的点的坐标可能是(D)

A.$(a,b)$
B.$(-a,b)$
C.$(-a,-b)$
D.$(a,-b)$

答案： D
解：
∵ ab ＞ 0，
∴ a，b 同号。
∵ a + b ＞ 0，
∴ a ＞ 0，b ＞ 0。
由图可知，小手盖住的点在第四象限，其坐标特征为（正，负）。
A. (a,b)：（正，正），第一象限，不符合；
B. (-a,b)：（负，正），第二象限，不符合；
C. (-a,-b)：（负，负），第三象限，不符合；
D. (a,-b)：（正，负），第四象限，符合。
答案：D

4. 在平面直角坐标系中，已知点$A(-1,3)$，$B(2,1)$，经过点$A$的直线$a// x$轴，$C$是直线$a$上的一个动点。当线段$BC$的长度最短时，点$C$的坐标为(C)

A.$(-1,1)$
B.$(3,2)$
C.$(2,3)$
D.$(2,-1)$

答案： C
解：
∵直线a//x轴且经过点A(-1,3)，
∴直线a上所有点的纵坐标均为3，设点C的坐标为(x,3)。
∵点到直线的垂线段最短，当BC⊥直线a时，线段BC长度最短。
∵直线a//x轴，
∴BC⊥x轴，此时点B与点C的横坐标相同。
∵点B的坐标为(2,1)，
∴x=2，即点C的坐标为(2,3)。
答案：C

5. 如果点$A(-1,m)$在$x$轴上，那么点$B(m - 1,m + 1)$的坐标为(-1,1)。

答案： (-1，1)
解：因为点A(-1,m)在x轴上，所以m=0。
则m-1=0-1=-1，m+1=0+1=1。
所以点B的坐标为(-1,1)。
答案：(-1,1)

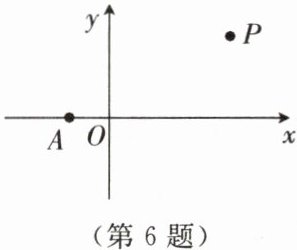
6. 如图，在平面直角坐标系的第一象限内有一点$P$，其横坐标为$3$，在$x$轴上有一点$A(-1,0)$。若$P$，$A$两点间的距离为$2\sqrt{5}$，则点$P$的纵坐标为2。

答案： 2
【解析】：
本题可根据平面直角坐标系中两点间的距离公式来求解点P的纵坐标。
设点P的坐标为$(3,y)（y\gt0，$因为点P在第一象限），已知点A(-1,0)，且P，A两点间的距离为$2\sqrt{5}。$
根据两点间距离公式$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}（$其中d为两点间的距离，$(x_1,y_1)，$$(x_2,y_2)$为两点的坐标），可得$\sqrt{(3 - (-1))^2 + (y - 0)^2} = 2\sqrt{5}。$
接下来求解上述方程：
首先对等式两边同时平方，得到$(3 - (-1))^2 + (y - 0)^2 = (2\sqrt{5})^2。$
然后化简方程：
$(3 + 1)^2 + y^2 = 20，$即$16 + y^2 = 20。$
接着移项可得$y^2 = 20 - 16 = 4。$
最后开平方，因为$y\gt0，$所以y = 2。
【答案】：
2

7. 若点$P$的坐标为$(3 - a,2a + 6)$，且点$P$到两坐标轴的距离相等，则点$P$的坐标是(12,-12)或(4,4)。

答案： (4， 4)或(12， -12)
解：
∵点P到两坐标轴的距离相等，
∴|3 - a| = |2a + 6|。
∴3 - a = 2a + 6或3 - a = -(2a + 6)。
当3 - a = 2a + 6时，
a - 2a = 6 - 3
3a = 3
a = -1。
此时3 - a = 4，2a + 6 = 4，点P的坐标为(4, 4)。
当3 - a = -(2a + 6)时，
3 - a = -2a - 6
a + 2a = -6 - 3
a = -9。
此时3 - a = 12，2a + 6 = -12，点P的坐标为(12, -12)。
综上，点P的坐标是(4, 4)或(12, -12)。

8. 已知点$P$的坐标为$(2m + 4,m - 1)$。根据下列条件，求点$P$的坐标。
（1）点$P$在$x$轴上。
（2）点$P$在第四象限，且到$x$轴的距离是到$y$轴距离的$2$倍。

答案： 解：​
(1)​根据题意，得​m-1=0​
解得​m=1​
∴​2m+4=2×1+4=6​
∴点​P ​的坐标为​(6，​​0)​
​
(2)​根据题意，得$​\begin {cases}{2\ \mathrm {m}+4＞0}\\{m-1＜0}\end {cases}​$
且​|m-1|=2 |$2\ \mathrm {m}+4$|，​
解得$​m=-\frac 75​$
∴$​2\ \mathrm {m}+4=\frac 65，$$​​m-1=-\frac {12}5​$
∴点​P ​的坐标为$​(\frac 65，$$​​-\frac {12}5)​$
【解析】：
本题主要考查了点与坐标轴的位置关系以及点到坐标轴的距离。
(1) 对于点P在x轴上的情况，由于x轴上的点的纵坐标为0，所以有m - 1 = 0，解得m = 1。
代入点P的横坐标得2m + 4 = 2 × 1 + 4 = 6，所以点P的坐标为(6, 0)。
(2) 对于点P在第四象限且到x轴的距离是到y轴距离的2倍的情况，由于第四象限的点横坐标为正，纵坐标为负，所以有m - 1 ＜ 0，即m ＜ 1。
点P到x轴的距离为|m - 1|，到y轴的距离为|2m + 4|。
根据题意，|m - 1| = 2|2m + 4|。
由于m ＜ 1，所以m - 1 ＜ 0，2m + 4 ＞ 0，可以去掉绝对值符号，得到1 - m = 2(2m + 4)。
解这个方程，得到$m = - \frac{7}{5}。$
代入点P的坐标得$2m + 4 = 2 × (-\frac{7}{5}) + 4 = \frac{6}{5}，$$m - 1 = -\frac{7}{5} - 1 = -\frac{12}{5}。$
所以点P的坐标为$(\frac{6}{5}, -\frac{12}{5})。$
【答案】：
(1) 点P的坐标为(6, 0)。
(2) 点P的坐标为$(\frac{6}{5}, -\frac{12}{5})。$