《2025年作业本江西教育出版社八年级数学上册北师大版》

1. 已知 A，B 两件衣服的成本共 500 元，某服装店老板分别以 30%和 20%的利润率定价后进行销售，共获利 130 元。两件衣服的成本分别为(A)

A.300 元，200 元
B.200 元，300 元
C.250 元，250 元
D.240 元，260 元

答案： A
解：设A衣服的成本为x元，B衣服的成本为y元。
根据题意，得$\begin{cases}x + y = 500 \\ 0.3x + 0.2y = 130\end{cases}$
由第一个方程得y = 500 - x，代入第二个方程：
0.3x + 0.2(500 - x) = 130
0.3x + 100 - 0.2x = 130
0.1x = 30
x = 300
则y = 500 - 300 = 200
答：A衣服成本300元，B衣服成本200元，选A。

2. 有两个旅游团去某航天科技馆参观。第一个旅游团有 15 名成人和 10 名儿童，共花费门票 850 元；第二个旅游团有 40 名成人和 50 名儿童，由于人数较多，成人票打八折，儿童票打六折，共花费 2030 元。成人票每张原价为40元，儿童票每张原价为25元。

答案： 40
25
【解析】：
本题考查二元一次方程组的应用。
设成人票每张原价为x元，儿童票每张原价为y元。
根据第一个旅游团的门票花费，我们可以得到第一个方程：
15x + 10y = 850，
根据第二个旅游团的门票花费，并且成人票打八折，儿童票打六折，我们可以得到第二个方程：
40x × 0.8 + 50y × 0.6 = 2030，
即：
32x + 30y = 2030，
接下来，我们解这个二元一次方程组：
我们可以将第一个方程乘以3，第二个方程乘以-1，然后相加，以消去y：
3(15x + 10y) - (32x + 30y) = 3 × 850 - 2030，
45x + 30y - 32x - 30y = 2550 - 2030，
13x = 520，
x = 40，
将x = 40代入第一个方程15x + 10y = 850，解得：
15 × 40 + 10y = 850，
600 + 10y = 850，
10y = 250，
y = 25，
所以，成人票每张原价为40元，儿童票每张原价为25元。
【答案】：
40；25。

3. 有一项生产 154 个零件的任务。若先由甲单独工作 5 天，然后乙加入与甲一起工作 3 天，则可以超额完成 2 个零件；若先由乙单独工作 5 天，然后甲加入与乙一起工作 3 天，则还差 13 个零件未能完成。甲每天生产15个零件，乙每天生产12个零件。

答案： 15
12
解：设甲每天生产x个零件，乙每天生产y个零件。
根据题意，得：
$\begin{cases}5x + 3(x + y) = 154 + 2 \\5y + 3(x + y) = 154 - 13\end{cases}$
化简方程组：
$\begin{cases}8x + 3y = 156 \\3x + 8y = 141\end{cases}$
将第一个方程乘以8，第二个方程乘以3：
$\begin{cases}64x + 24y = 1248 \\9x + 24y = 423\end{cases}$
两式相减：55x = 825，解得x = 15。
将x = 15代入8x + 3y = 156：120 + 3y = 156，解得y = 12。
甲每天生产15个零件，乙每天生产12个零件。
15；12

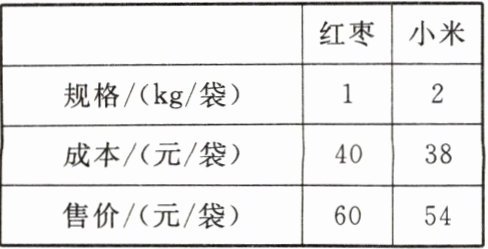
4. 为解决山区土特产销售问题，某地政府帮助小强家开通了网络销售渠道，将红枣、小米等农产品销往全国。已知今年前三个月共销售红枣和小米共 3000 kg，获得利润 4.2 万元，具体销售情况如下表所示。这三个月共销售红枣1500袋，小米750袋。

答案： 1500
750
【解析】：
本题考查二元一次方程组的应用，我们可以通过设未知数，根据销售的总重量和总利润列出方程组，进而求解出红枣和小米的销售袋数。
设这三个月共销售红枣x袋，销售小米y袋。
步骤一：根据销售的总重量列出方程
已知红枣每袋1kg，小米每袋2kg，且前三个月共销售红枣和小米共3000kg，可得到方程x + 2y = 3000。
步骤二：根据获得的总利润列出方程
先分别计算出每袋红枣和每袋小米的利润：
每袋红枣的成本是40元，售价是60元，所以每袋红枣的利润为60 - 40 = 20元。
每袋小米的成本是38元，售价是54元，所以每袋小米的利润为54 - 38 = 16元。
已知前三个月获得利润4.2万元，因为1万元 = 10000元，所以4.2万元 = 4.2×10000 = 42000元，可得到方程20x + 16y = 42000。
步骤三：联立方程组并求解
联立上述两个方程可得方程组$\begin{cases}x + 2y = 3000\\20x + 16y = 42000\end{cases}$
由第一个方程x + 2y = 3000可得x = 3000 - 2y，将其代入第二个方程20x + 16y = 42000中：
$\begin{aligned}20×(3000 - 2y) + 16y&= 42000\\60000 - 40y + 16y&= 42000\\40y + 16y&= 42000 - 60000\\24y&= - 18000\\y&= 750\end{aligned}$
将y = 750代入x = 3000 - 2y可得：
x = 3000 - 2×750 = 3000 - 1500 = 1500
【答案】：
这三个月共销售红枣1500袋，小米750袋。

5. 某商场计划购进一批香蕉和橙子。已知购进 2 kg 香蕉和 3 kg 橙子共需 46 元；购进 1 kg 香蕉和 2 kg 橙子共需 28 元。
（1）香蕉和橙子的进价分别是每千克多少元？
（2）该商场计划购进香蕉和橙子共 1000 kg。已知香蕉的售价为 12 元/kg，橙子的售价为 15 元/kg，其中香蕉的进货量不低于 350 kg，且不高于 450 kg。在可以全部售出的情况下，求总利润的最大值。

答案： 解：​
(1)​设香蕉的进价是​x​元$​/\mathrm {kg}，$​
橙子的进价是​y​元$​/\mathrm {kg}​$
根据题意得$​\begin {cases}{x+2y=28}\\{2x+3y=46}\end {cases}，$​解得$​\begin {cases}{x=8}\\{y=10}\end {cases}​$
答：香蕉的进价是​8​元$​/\mathrm {kg}，$​
橙子的进价是​10​元$​/\mathrm {kg}。$​
​
(2)​设购进$​m\mathrm {kg }{香蕉}，$​则购进$​(1000-m)\mathrm {kg }{橙子}，$​
全部售出后获得的总利润为​W {元}​
据题意得​W=(12-8)m+(15-10)·(1000-m)​
即​W=-m+5000​
∴​W {随}m ​的增大而减小
又
∵​350≤m≤450​
∴当​m=350​时，​W ​取得最大值，
最大值为​-350+5000=4650​
答：总利润的最大值是​4650​元。