《2025年作业本江西教育出版社八年级数学上册北师大版》

16. 已知 3 是 $ 2x + 1 $ 的算术平方根，-2 是 $ -3x + y + 5 $ 的立方根，求 $ x - y $ 的平方根。

答案： 解：依题意，得$​\sqrt {2x+1}=3​$
解得​x=4​
由$​\sqrt [3]{-3x+y+5}=-2​$
得​-12+y+5=-8​
解得​y=-1​
∴$​ \sqrt {x-y}= \sqrt {4-(-1)}= \sqrt 5​$

17. 小明在物理课上学习了发声物体的振动实验后，对此进行了进一步的探究：在一个支架的横杆点 O 处用一根细绳悬挂一个小球 A，小球 A 可以自由摆动，如图①，OA 表示小球静止时的位置。当小明用发声物体靠近小球时，小球从 OA 摆到 OB 的位置，如图②。过点 B 作 $ BD \perp OA $ 于点 D，当小球摆到 OC 的位置时，OB 与 OC 恰好垂直（图②中的点 A，B，O，C 在同一平面上）。过点 C 作 $ CE \perp OA $ 于点 E，测得 $ BD = 8 cm $，$ OA = 17 cm $，求 DE 的长。

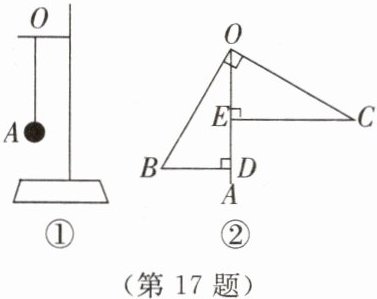
答案： 解：
∵​OB⊥OC​
∴​∠BOD+∠COE=90°​
又
∵​CE⊥OA，​​BD⊥OA​
∴​∠CEO=∠ODB=90°​
∴​∠BOD+∠B=90°​
∴​∠COE=∠B​
在​△COE ​和​△OBD ​中
$​\begin {cases}{∠CEO=∠ODB}\\{∠COE=∠B}\\{OC=BO}\end {cases}​$
∴$​△COE≌△ OBD(\mathrm {AAS})​$
∴​OE=BD=8 {cm}​
在​ Rt△BDO ​中，由勾股定理，
得$​ OD=\sqrt {OB^2-BD^2}=\sqrt {OA^2-BD^2}​$
$​=\sqrt {17^2-8^2}=15({cm})​$
∴​DE=OD-OE=15-8=7({cm})​

18. 如图，在平面直角坐标系中，已知点 $ A(5,2) $，$ B(1,5) $，$ C(-4,-3) $。
（1）作出 $ \triangle ABC $，并作出 $ \triangle ABC $ 关于 x 轴对称的 $ \triangle A'B'C' $。
（2）在 x 轴上找一点 P，使得 $ AP + PB $ 的值最小，求出点 P 的坐标。

答案：

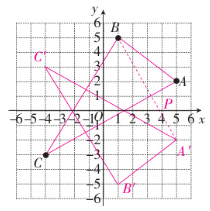
解：​
(1)​如图所示，​∆ABC​和​∆A'B'C'​即为
所求作的三角形
​
(2)​连接​A'B，​与​x​轴交于点​P，​
点​P ​即为所求的点
设直线​A'B​的表达式为​y = kx + b​
∵点​A'​和点​B​的坐标分别为​(5，​​-2)，​​(1，​​5)，​
∴$​\begin {cases}{5k+b=-2}\\{k+b=5}\end {cases}，$​解得$​\begin {cases}{k=-\frac 74}\\{b=\frac {27}4 }\end {cases}​$
∴直线​A'B​的表达式为$​y=-\frac 74x+\frac {27}4​$
当​y = 0​时，$​0=-\frac 74x+\frac {27}4​$
解得$​x=\frac {27}7​$
∴点​P ​的坐标为$​(\frac {27}7，$​​0)​