《2025年作业本江西教育出版社八年级数学上册北师大版》

1. 直线 $ y = kx + 5(k \neq 0) $ 与 $ x $ 轴交于点 $ (-5,0) $。下列说法正确的是(D)

A.$ k \lt 0 $
B.已知直线上两点 $ (x_1,y_1) $，$ (x_2,y_2) $，若 $ x_1 \lt x_2 $，则 $ y_1 \gt y_2 $
C.直线经过第四象限
D.关于 $ x $ 的方程 $ kx + 5 = 0 $ 的解为 $ x = -5 $

答案： D
【解析】：
本题主要考察一次函数的性质以及一次函数与坐标轴交点的意义。
首先，根据题目条件，直线$y = kx + 5（k \neq 0）$与x轴交于点(-5, 0)。
代入该点的坐标到直线方程中，即0 = -5k + 5，
解得k = 1。
接下来，逐一分析选项：
A. k ＜ 0
由于已经求出k = 1，显然k不小于0，所以A选项错误。
B. 已知直线上两点$(x_1, y_1)，$$(x_2, y_2)，$若$x_1 ＜ x_2，$则$y_1 ＞ y_2$
由于k = 1 ＞ 0，根据一次函数的性质，当k ＞ 0时，y随x的增大而增大。
因此，若$x_1 ＜ x_2，$则应有$y_1 ＜ y_2，$所以B选项错误。
C. 直线经过第四象限
由于k = 1 ＞ 0且b = 5 ＞ 0，根据一次函数的图像性质，该直线将经过第一、二、三象限，不经过第四象限。
所以C选项错误。
D. 关于x的方程kx + 5 = 0的解为x = -5
由于已经求出k = 1，代入方程kx + 5 = 0，得到x + 5 = 0，解得x = -5。
所以D选项正确。
【答案】：
D

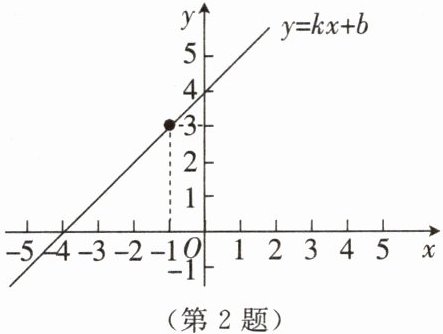
2. 如图，若直线 $ y = kx + b(k \neq 0) $ 经过点 $ (-1,3) $，则方程 $ kx + b = 3 $ 的解为(A)

A.$ x = -1 $
B.$ x = 3 $
C.$ x = -4 $
D.$ x = 4 $

答案： A
【解析】：本题主要考查了一次函数与一元一次方程的关系。
我们知道，一次函数$y = kx + b（k\neq0）$与一元一次方程kx + b = c（c为常数）有紧密联系。
一次函数$y = kx + b（k\neq0）$中，当y取某一确定值时，就得到一个关于x的一元一次方程。
在本题中，直线$y = kx + b（k\neq0）$经过点(-1,3)，这意味着当x = -1时，y的值为3，即把x = -1代入一次函数y = kx + b中，可得y=k×(-1)+b = 3。
而方程kx + b = 3就是求当y = 3时x的值，由于直线经过点(-1,3)，所以x的值就是-1，即方程kx + b = 3的解为x = -1。
【答案】：A。

3. 若关于 $ x $ 的方程 $ ax + b = 2 $ 的解为 $ x = -5 $，则一次函数 $ y = ax + b - 2 $ 的图象与 $ x $ 轴交点的坐标为(-5,0)。

答案： (-5， 0)
解：因为关于x的方程ax + b = 2的解为x = -5，所以将x = -5代入方程得：-5a + b = 2。
对于一次函数y = ax + b - 2，令y = 0，则ax + b - 2 = 0，即ax + b = 2。
由已知，方程ax + b = 2的解为x = -5，所以一次函数y = ax + b - 2的图象与x轴交点的横坐标为-5。
故交点坐标为(-5, 0)。
答案：(-5, 0)

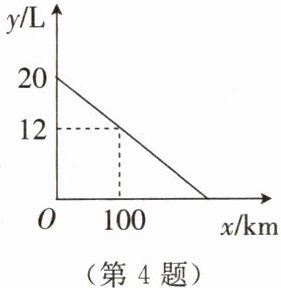
4. 某品牌汽车油箱的容量为 $ 20 \, L $。油箱中剩余油量 $ y $(单位：$ L $)与汽车行驶路程 $ x $(单位：$ km $)之间的关系如图所示。$ 10 \, L $ 汽油可供该汽车行驶125 $ km $。

答案： 125
【解析】：本题考查了一次函数在实际问题中的应用，通过图像获取信息来求解问题。
从图像中可知，当x = 0时，y = 20，即汽车初始油量为20L；当x = 100时，y = 12。
设y与x的函数关系式为y=kx+b（k，b为常数），把(0,20)，(100,12)代入可得：
$\begin{cases}b = 20\\100k + b = 12\end{cases}$
将b = 20代入100k + b = 12，得100k+20 = 12，
移项可得100k=12 - 20=-8，
解得$k=-\frac{8}{100}=-0.08。$
所以y与x的函数关系式为y=-0.08x + 20。
要求10L汽油可供汽车行驶的路程，即当y = 10时，求x的值。
把y = 10代入y=-0.08x + 20，得10=-0.08x + 20，
移项可得0.08x=20 - 10 = 10，
解得x = 125。
【答案】：125

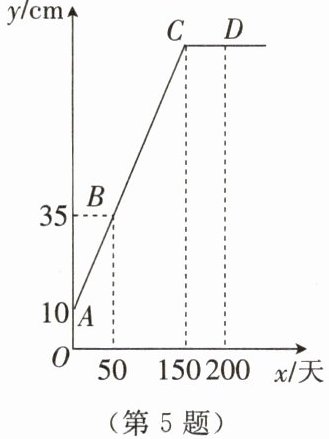
5. 生物活动小组的同学们观察某植物生长，得到该植物高度 $ y $（单位：$ cm $）与观察时间 $ x $（单位：天）的关系，画出如图所示的函数图象 $ (CD // x $ 轴)。
(1) 观察前植物的高度是多少厘米？
(2) 求线段 $ AC $ 对应的函数表达式。（不要求写出自变量 $ x $ 的取值范围）
(3) 观察 $ 180 $ 天后，该植物的高度是多少厘米？

答案： 解：​
(1) ​观察前植物的高度为$​ 10\ \mathrm {cm}​$
​
(2) ​设线段​ AC ​对应的函数表达式是​ y=kx+b​
则$​\begin {cases}{b=10}\\{50k+b=35}\end {cases}，$​解得$​\begin {cases}{b=10}\\{k=0.5}\end {cases}​$
∴线段​ AC ​对应的函数表达式是​ y=0.5x+10​
​
(3)​由图知，该植物从观察时起​ 150 ​天后停止生长
当​ x=150 ​时，​y=0.5×150+10=85​
∴观察​ 180 ​天后，该植物的高度是$​ 85\ \mathrm {cm}​$