第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 某运动员在跳水比赛中的得分如下:8.5,8.5,8.5,9.5,9.0,9.0,9.0。他本次得分的平均成绩和中位数分别为(
A.$\frac{62}{7}$,8.75
B.$\frac{62}{7}$,9.0
C.8.8,8.75
D.8.8,9.0
B
)A.$\frac{62}{7}$,8.75
B.$\frac{62}{7}$,9.0
C.8.8,8.75
D.8.8,9.0
答案:
B
【解析】:
本题主要考查中位数和平均数的计算。
首先,计算平均成绩。
平均成绩是所有成绩之和除以成绩的数量。
给定的成绩是:8.5, 8.5, 8.5, 9.5, 9.0, 9.0, 9.0,
平均成绩为:
平均成绩$ = \frac{8.5 + 8.5 + 8.5 + 9.5 + 9.0 + 9.0 + 9.0}{7} = \frac{62}{7} \approx 8.857 \approx 8.8($四舍五入),
但考虑到题目中的选项,我们将其转化为分数形式,即$\frac{62}{7},$或保留一位小数,即8.8(根据四舍五入)。
接着,计算中位数。
中位数是将一组数据从小到大排序后,位于中间的数。
如果数据量是奇数,则中位数是中间的那个数;
如果数据量是偶数,则中位数是中间两个数的平均值。
将数据从小到大排序:8.5, 8.5, 8.5, 9.0, 9.0, 9.0, 9.5,
因为数据量是奇数(7个),所以中位数就是排序后的第4个数,即9.0。
综合以上计算,平均成绩为$\frac{62}{7}($或8.8),中位数为9.0。
【答案】:
$B. \frac{62}{7}, 9.0。$
【解析】:
本题主要考查中位数和平均数的计算。
首先,计算平均成绩。
平均成绩是所有成绩之和除以成绩的数量。
给定的成绩是:8.5, 8.5, 8.5, 9.5, 9.0, 9.0, 9.0,
平均成绩为:
平均成绩$ = \frac{8.5 + 8.5 + 8.5 + 9.5 + 9.0 + 9.0 + 9.0}{7} = \frac{62}{7} \approx 8.857 \approx 8.8($四舍五入),
但考虑到题目中的选项,我们将其转化为分数形式,即$\frac{62}{7},$或保留一位小数,即8.8(根据四舍五入)。
接着,计算中位数。
中位数是将一组数据从小到大排序后,位于中间的数。
如果数据量是奇数,则中位数是中间的那个数;
如果数据量是偶数,则中位数是中间两个数的平均值。
将数据从小到大排序:8.5, 8.5, 8.5, 9.0, 9.0, 9.0, 9.5,
因为数据量是奇数(7个),所以中位数就是排序后的第4个数,即9.0。
综合以上计算,平均成绩为$\frac{62}{7}($或8.8),中位数为9.0。
【答案】:
$B. \frac{62}{7}, 9.0。$
2. 在一组数据 21,30,8,5,20 中插入一个数,恰好得中位数是 19,插入的数是
18
。
答案:
18
解:将原数据排序:5,8,20,21,30
插入一个数后数据共6个,中位数为中间两数的平均数,设插入的数为x。
排序后中间两数之和需为19×2=38。
分情况讨论:
1. 若x≤8,排序为x,5,8,20,21,30,中间两数8和20,和为28≠38;
2. 若8<x≤20,排序为5,8,x,20,21,30,中间两数x和20,x+20=38,解得x=18;
3. 若x>20,排序为5,8,20,x,21,30,中间两数20和x,20+x=38,解得x=18(矛盾,舍去)。
插入的数是18。
答案:18
解:将原数据排序:5,8,20,21,30
插入一个数后数据共6个,中位数为中间两数的平均数,设插入的数为x。
排序后中间两数之和需为19×2=38。
分情况讨论:
1. 若x≤8,排序为x,5,8,20,21,30,中间两数8和20,和为28≠38;
2. 若8<x≤20,排序为5,8,x,20,21,30,中间两数x和20,x+20=38,解得x=18;
3. 若x>20,排序为5,8,20,x,21,30,中间两数20和x,20+x=38,解得x=18(矛盾,舍去)。
插入的数是18。
答案:18
3. 为了解某校八年级男生在体能测试中引体向上项目的情况,随机抽取了该校部分男生引体向上项目的测试成绩,并绘制成如图所示的统计图。请根据图中信息,解答下列问题。
(1)本次接受抽样调查的男生人数为
(2)本次调查获取的样本数据的众数为
(3)完成引体向上项目的测试成绩百分位数值表。
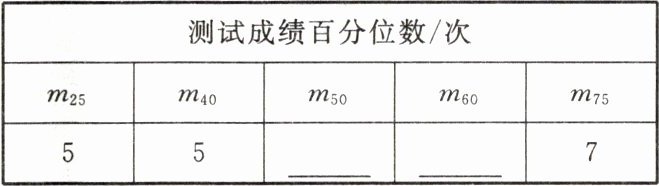
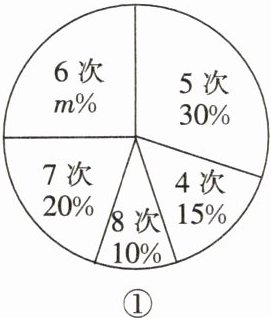
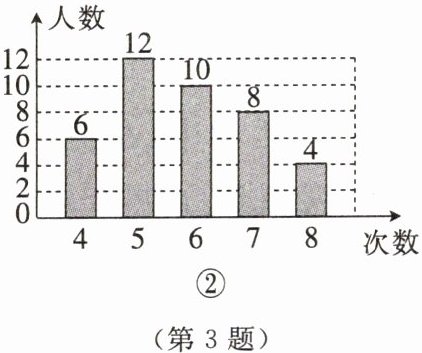
(1)本次接受抽样调查的男生人数为
40
,图①中$m$的值为25
。(2)本次调查获取的样本数据的众数为
5次
,中位数为6次
。(3)完成引体向上项目的测试成绩百分位数值表。



答案:
(1)40 25
(2)5次 6次
(3)6 6
(2)5次 6次
(3)6 6
4. 某车间共有 15 名技术工人,为了合理制订每月加工零件的数量,现随机统计了他们某个月加工的零件数,具体数据如下表所示:

(1)这 15 名工人该月加工零件数的平均数为______,中位数为______,众数为______。
(2)若将该车间每名工人的月加工零件数定为 260,你认为是否合理?为什么?

(1)这 15 名工人该月加工零件数的平均数为______,中位数为______,众数为______。
(2)若将该车间每名工人的月加工零件数定为 260,你认为是否合理?为什么?
答案:
(1)260件
240件
240件
(2)解:
不合理。理由如下:
根据表中数据,每月能完成260件的只有4人,
还有11人不能达到此数量,由于少数高产量
工人的数据拉高了整体平均数,将定额定
为260件会导致大多数工人无法完成生产任务,
既不符合实际生产水平,也不利于调动
员工的积极性。
240件
240件
(2)解:
不合理。理由如下:
根据表中数据,每月能完成260件的只有4人,
还有11人不能达到此数量,由于少数高产量
工人的数据拉高了整体平均数,将定额定
为260件会导致大多数工人无法完成生产任务,
既不符合实际生产水平,也不利于调动
员工的积极性。
查看更多完整答案,请扫码查看


