《2025年作业本江西教育出版社八年级数学上册北师大版》

16. 如图，在平面直角坐标系中，$\triangle A_1B_1C_1$与$\triangle ABC$关于$y$轴对称。
(1) 在图中画出$\triangle A_1B_1C_1$，并写出点$A_1$，$B_1$的坐标。
(2) 试判断$\triangle ABC$的形状，并说明理由。

答案：

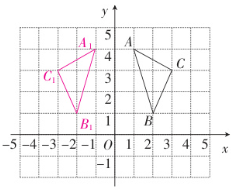
解：$​(1)∆A_{1}B_{1}C_{1}​$即为所求作的三角形
$​A_{1}(-1，$​​4)，$​​B_{1}(-2，$​​1)​
​
(2)∆ABC​是等腰直角三角形，理由如下：
∵$​AC^2 = 5，$$​​AB^2 = 10，$$​​BC^2 = 5​$
即$​AB^2 = AC^2 + BC^2，$​且​AC = BC​
∴​∆ABC​是等腰直角三角形

17. 如图，已知一次函数$y = kx - 3$的图象经过点$M(-2,1)$，且与$x$轴、$y$轴分别交于点$A$，$B$。
(1) 求$k$的值。
(2) 求$\triangle ABO$的面积。

答案： 解：​
(1)​
∵一次函数​ y=kx-3 ​的图象
经过点​ M(-2，​​1)​
∴​1=-2k-3​
解得​ k=-2​
​
(2) ​由​
(1)​可知，直线​ AB ​的表达式为​ y=-2x-3​
当​ x=0 ​时，​y=-2×0-3=-3​
∴点​ B ​的坐标为​ (0，​​-3)​
∴​OB=3​
当​ y=0 ​时，​-2x-3=0​
解得$​ x=-\frac 32​$
∴点​ A ​的坐标为$​ (-\frac 32，$​​0)​
∴$​OA=\frac 32​$
∴$​S_{△ABO}=\frac 12OA·OB​$
$​=\frac 12×\frac 32×3=\frac 94​$

18. 如图，点$P(-2,4)$，$M(-1,1)$关于直线$x = 1$的对称点分别为$P'$，$M'$。
(1) 点$P'$的坐标为(4,4)，点$M'$的坐标为(3,1)。
(2) 点$P(-2,4)$关于直线$x = -1$对称的点的坐标为(0,4)；点$N(5,-2)$关于直线$x = 2$对称的点的坐标为(−1,−2)。
(3) 求点$(a,b)$关于直线$x = n$对称的点的坐标。

答案： (3，1)
(4，4)
(0，4)
(-1，-2)
解：​
(3)​设对称点的坐标为​(x，​​y)​
则有$​\frac {a+x}2=n，$​​y=b​
∴​x=2n-a​
∴点​(a，​​b)​关于直线​x=n​对称的
点的坐标为​(2n-a，​​b)​