《2025年作业本江西教育出版社八年级数学上册北师大版》

1. 以下列各组数为边长，不能构成直角三角形的是(B)

A.$3$，$4$，$5$
B.$2$，$3$，$4$
C.$5$，$12$，$13$
D.$1$，$\sqrt{2}$，$\sqrt{3}$

答案： B
【解析】：
本题考察的是勾股定理的逆定理，即如果三角形三边满足勾股定理，即最长边的平方等于其他两边的平方和，则这个三角形是直角三角形。
我们需要分别验证每一组数是否满足勾股定理。
A. 对于3，4，5，有$3^2 + 4^2 = 9 + 16 = 25 = 5^2，$满足勾股定理，故是直角三角形。
B. 对于2，3，4，有$2^2 + 3^2 = 4 + 9 = 13 \neq 4^2，$不满足勾股定理，故不是直角三角形。
C. 对于5，12，13，有$5^2 + 12^2 = 25 + 144 = 169 = 13^2，$满足勾股定理，故是直角三角形。
D. 对于1，$\sqrt{2}，$$\sqrt{3}，$有$1^2 + (\sqrt{2})^2 = 1 + 2 = 3 = (\sqrt{3})^2，$满足勾股定理，故是直角三角形。
因此，不能构成直角三角形的是B选项。
【答案】：
B

2. 有下列函数关系式：①$y = kx$；②$y=\frac{3}{x}$；③$y=\frac{2}{3}x$；④$y = x^2-(x - 1)(x + 2)$；⑤$y = 4 - x$。其中一定是一次函数的有(B)

A.$4$个
B.$3$个
C.$2$个
D.$1$个

答案： B
【解析】：
首先，我们需要明确一次函数的定义：一次函数是形如y=kx+b的函数，其中k和b为常数，且$k \neq 0。$
对于给定的函数关系式进行逐一判断：
①y = kx：当$k \neq 0$时，它是一次函数。但题目没有明确k的取值范围，若k=0，则不是一次函数，因此，不能确定它一定是一次函数。
$②y = \frac{3}{x}$：这是反比例函数的形式，不是一次函数。
$③y = \frac{2}{3}x$：可以写成y=kx的形式，其中$k=\frac{2}{3} \neq 0，$所以它是一次函数。
$④y = x^2 - (x-1)(x+2)$：
首先展开并化简：
$y = x^2 - (x^2 + x - 2)$
$y = x^2 - x^2 - x + 2$
y = -x + 2
这是形如y=kx+b的形式，其中$k=-1 \neq 0，$b=2，所以它是一次函数。
⑤y = 4-x：可以写成y=kx+b的形式，其中k=-1，b=4，且$k \neq 0，$所以它是一次函数。
综上所述，一定是一次函数的有③、④、⑤三个，但由于①的不确定性，我们只计算确定的一次函数。
【答案】：B. 3个。

3. 有下列各数：$3.141592$，$-\sqrt{3}$，$0.16$，$\sqrt{10^2}$，$-\pi$，$0.1010010001·s$(相邻两个$1$之间$0$的个数逐次加$1$)，$\frac{22}{7}$，$\sqrt[3]{5}$，$0.\dot{2}$，$\sqrt{8}$。其中无理数有(A)

A.$5$个
B.$3$个
C.$4$个
D.$2$个

答案： A
解：无理数是无限不循环小数。
3.141592是有限小数，不是无理数；
$-\sqrt{3}$是无限不循环小数，是无理数；
0.16是有限小数，不是无理数；
$\sqrt{10^2}=10$是整数，不是无理数；
$-\pi$是无限不循环小数，是无理数；
0.1010010001…（相邻两个1之间0的个数逐次加1）是无限不循环小数，是无理数；
$\frac{22}{7}$是分数，不是无理数；
$\sqrt[3]{5}$是无限不循环小数，是无理数；
0.2是有限小数，不是无理数；
$\sqrt{8}=2\sqrt{2}$是无限不循环小数，是无理数。
综上，无理数有$-\sqrt{3},-\pi,0.1010010001…,\sqrt[3]{5},\sqrt{8}，$共5个。
答案：A

4. 下列运算正确的是(B)

A.$\sqrt{2}+\sqrt{4}=\sqrt{6}$
B.$\sqrt{18}-\sqrt{8}=\sqrt{2}$
C.$\sqrt{9}=\pm3$
D.$\sqrt{5}÷\sqrt{\frac{1}{5}}=\frac{1}{5}$

答案： B
【解析】：
本题主要考察二次根式的加减运算以及二次根式的性质和化简。
A选项：$\sqrt{2}+\sqrt{4}，$其中$\sqrt{4}$可以化简为2，所以$\sqrt{2}+\sqrt{4}=\sqrt{2}+2，$显然不等于$\sqrt{6}，$所以A选项错误。
B选项：$\sqrt{18}-\sqrt{8}，$其中$\sqrt{18}$可以化简为$3\sqrt{2}，$$\sqrt{8}$可以化简为$2\sqrt{2}，$所以$\sqrt{18}-\sqrt{8}=3\sqrt{2}-2\sqrt{2}=\sqrt{2}，$B选项正确。
C选项：根据算术平方根的定义，$\sqrt{9}$表示9的非负平方根，所以$\sqrt{9}=3，$并不等于$\pm3，$C选项错误。
D选项：$\sqrt{5}÷\sqrt{\frac{1}{5}}，$根据二次根式的除法法则，可以化简为$\sqrt{5} × \sqrt{5}=5，$显然不等于$\frac{1}{5}，$所以D选项错误。
【答案】：
B

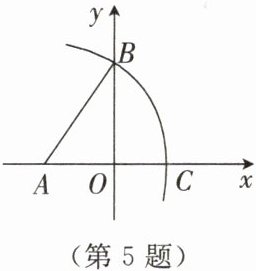
5. 如图，在平面直角坐标系中，已知点$A(-2,0)$，$B(0,3)$。以点$A$为圆心，$AB$长为半径作弧，交$x$轴的正半轴于点$C$，则点$C$的横坐标为(A)

A.$\sqrt{13}-2$
B.$\sqrt{13}$
C.$\sqrt{13}+2$
D.$-\sqrt{13}+2$

答案： A
【解析】：本题可先根据两点间距离公式求出AB的长度，即圆A的半径，再设点C的横坐标，根据点C在x轴正半轴以及AC的长度等于圆A的半径列出方程，进而求解点C的横坐标。
步骤一：求AB的长度
已知点A(-2,0)，B(0,3)，根据两点间距离公式$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}（$其中$(x_1,y_1)，$$(x_2,y_2)$为两点的坐标，d为两点间的距离），可得：
$AB=\sqrt{(0 - (-2))^2 + (3 - 0)^2}=\sqrt{2^2 + 3^2}=\sqrt{4 + 9}=\sqrt{13}$
因为以点A为圆心，AB长为半径作弧，所以圆A的半径$r = AB = \sqrt{13}。$
步骤二：设点C的横坐标并表示出AC的长度
设点C的横坐标为$x（x\gt0），$因为点A的横坐标为-2，且点C在x轴上，所以AC的长度为$\vert x - (-2)\vert=\vert x + 2\vert，$又因为$x\gt0，$所以$x + 2\gt0，$则AC = x + 2。
步骤三：根据AC的长度等于圆A的半径列方程求解
由于AC的长度等于圆A的半径$\sqrt{13}，$所以可得方程$x + 2 = \sqrt{13}，$移项可得$x = \sqrt{13} - 2，$即点C的横坐标为$\sqrt{13} - 2。$
【答案】：A

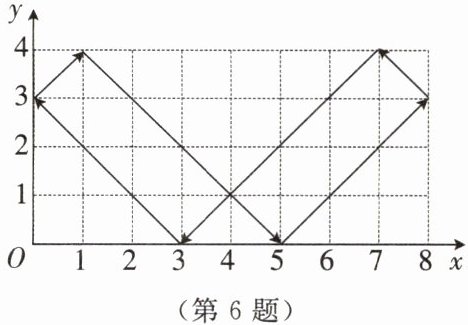
6. 一个小球起始时位于$(3,0)$处，按指定方向击出后，其运动轨迹如图所示。如果小球起始时位于$(1,0)$处，仍按原来方向击球，小球第一次碰到球桌边时，小球的位置是$(0,1)$，那么小球第$2024$次碰到球桌边时，小球的位置是(A)

A.$(3,4)$
B.$(5,4)$
C.$(7,0)$
D.$(8,1)$

答案： A

7. $\sqrt{25}$的算术平方根等于$\sqrt{5}$。

答案： $​\sqrt 5​$

8. 若$P_1(1,y_1)$，$P_2(2,y_2)$在一次函数$y = -x + 1$的图象上，则$y_1$＞$y_2$。(填“$＞$”“$＜$”或“$=$”)

答案： ＞
【解析】：
本题主要考察一次函数的单调性。
对于一次函数y = kx + b，其中k为斜率。
当k ＞ 0时，函数为增函数，即y随x的增大而增大；
当k ＜ 0时，函数为减函数，即y随x的增大而减小。
对于给定的函数y = -x + 1，其斜率k = -1 ＜ 0，所以这是一个减函数。
现在，我们有两个点$P_1(1,y_1)$和$P_2(2,y_2)$在该函数图象上。
由于1 ＜ 2，并且函数是减函数，所以对应的函数值$y_1$必然大于$y_2。$
【答案】：
＞

9. 在某中学实践活动课上，小丽打算测量学校旗杆的高度。她发现旗杆顶端的绳子垂到地面后还多出$1m$，当她把绳子斜拉直，且使绳子的底端刚好接触地面时，测得绳子底端距离旗杆底部$5m$。学校旗杆的高度是12$m$。

答案： 【解析】：
本题考查勾股定理的应用。要测量学校旗杆的高度，我们可以利用勾股定理来求解。
设旗杆的高度为x米，那么绳子的长度就是x+1米（因为绳子垂到地面后还多出1米）。
当绳子斜拉直，且使绳子的底端刚好接触地面时，测得绳子底端距离旗杆底部5米，这构成了一个直角三角形。
其中，旗杆的高度是直角边之一，长度为x米；
绳子底端距离旗杆底部的距离是另一直角边，长度为5米；
绳子的长度是斜边，长度为x+1米。
根据勾股定理，有：
$x^2 + 5^2 = (x + 1)^2$
展开并整理得：
$x^2 + 25 = x^2 + 2x + 1$
进一步整理，得：
2x = 24
解得：
x = 12
所以，学校旗杆的高度是12米。
【答案】：
12