《2025年作业本江西教育出版社八年级数学上册北师大版》

1. 下列实数是无理数的是(A)

A.$\frac{\pi}{2}$
B.$(\pi - 1)^{0}$
C.2
D.3.14

答案： A
【解析】：
本题主要考察无理数和有理数的定义和识别。无理数是不能表示为两个整数的比的数，且其小数部分是无限不循环的。有理数则可以表示为两个整数的比，且其小数部分要么是有限的，要么是无限循环的。
A选项：$\frac{\pi}{2}，$由于$\pi$是一个无理数，其任何非零有限倍仍然是无理数，所以$\frac{\pi}{2}$是无理数。
B选项：$(\pi - 1)^0，$任何非零数的0次方都是1，所以$(\pi - 1)^0 = 1，$是有理数。
C选项：2，是一个整数，整数都是有理数。
D选项：3.14，是一个有限小数，有限小数都是有理数。
综上所述，只有A选项是无理数。
【答案】：
A

2. 在0，$\pi$，0.010 110 111 0…(相邻两个0之间1的个数逐次加1)，3.14，$\frac{24}{11}$中，无理数有(C)

A.4个
B.3个
C.2个
D.1个

答案： C
【解析】：
本题主要考查无理数的定义。无理数是不能表示为两个整数的比值的数，且是无限不循环小数。
0 是整数，因此它是有理数。
$\pi $是一个著名的无理数，它不能表示为两个整数的比值，且是无限不循环的。
$0.0101101110\ldots（$相邻两个0之间1的个数逐次加1）这是一个无限不循环小数，
因此它是无理数。
3.14 是一个有限小数，因此它是有理数。
$\frac{24}{11}$是两个整数的比值，尽管它的小数形式是无限循环的，但它仍然是有理数。
综上所述，无理数有$ \pi $和$ 0.0101101110\ldots（$相邻两个0之间1的个数逐次加1）共2个。
【答案】：
C

3. 下列说法正确的是(D)

A.有理数与数轴上的点一一对应
B.无理数与数轴上的点一一对应
C.整数与数轴上的点一一对应
D.实数与数轴上的点一一对应

答案： D
【解析】：
本题主要考察实数与数轴的关系。根据数学知识，我们知道实数与数轴上的点是一一对应的，这包括有理数和无理数。而有理数、整数只是实数的一部分，它们并不能与数轴上的点一一对应。
A选项表示有理数与数轴上的点一一对应，这是不正确的，因为有理数只是实数的一部分，还包括无理数。
B选项表示无理数与数轴上的点一一对应，这也是不正确的，因为无理数也只是实数的一部分，还包括有理数。
C选项表示整数与数轴上的点一一对应，这同样是不正确的，因为整数也只是实数的一部分。
D选项表示实数与数轴上的点一一对应，这是正确的。
【答案】：
D

4. 下列说法正确的是(A)

A.有理数可以用有限小数或无限循环小数表示
B.无限小数就是无理数
C.不循环小数是无理数
D.0既不是有理数，也不是无理数

答案： A
【解析】：
本题主要考察有理数和无理数的定义及性质。
A选项：有理数的定义是可以表示为两个整数的比的数，其中分母不为0。有理数确实可以表示为有限小数或无限循环小数。例如，1/2=0.5（有限小数），1/3=0.333...（无限循环小数）。所以A选项正确。
B选项：无限小数包括无限循环小数和无限不循环小数。其中，只有无限不循环小数是无理数。因此，将无限小数等同于无理数是不准确的。所以B选项错误。
C选项：不循环小数确实是无理数的一种表现，但并非所有不循环小数都是无理数的完整描述。更准确的说法是，无限不循环小数是无理数。但考虑到此选项的表述可能意图指向此意，只是表述不严谨，按照题目要求，我们判定其为错误，因为存在有限不循环小数（如人为构造的特定小数），它们并不是无理数。但在此题的语境下，我们主要关注无限小数的情况，因此判断C选项错误，因为它没有明确指出“无限”。
D选项：0是整数，因此它自然也是有理数。所以D选项错误。
【答案】：
A

5. 下列说法正确的有(A)
①无理数包括正无理数，0和负无理数；②无理数都可以用数轴上的点来表示；③数轴上的点表示无理数；④有理数与数轴上的点是一一对应关系。

A.1个
B.2个
C.3个
D.4个

答案： A
【解析】：
本题主要考查了实数与数轴的关系以及无理数和有理数的概念。
① 对于无理数的定义，我们知道无理数是不能表示为两个整数的比的数，且它们在小数展开后是无限不循环的。无理数确实包括正无理数和负无理数，但0是有理数，
因此，此说法错误。
② 对于数轴上的点与实数的关系，我们知道每一个实数都可以用数轴上的一个点来表示，同时数轴上的每一个点也都表示一个实数。无理数作为实数的一个子集，自然也可以用数轴上的点来表示。
因此，此说法正确。
③ 数轴上的点不仅可以表示无理数，还可以表示有理数。有理数如整数、分数等都可以在数轴上找到对应的点。
因此，此说法错误，因为它忽略了数轴上的点还可以表示有理数。
④ 有理数与数轴上的点并不是一一对应关系，因为数轴上的点还可以表示无理数。实际上，实数（包括有理数和无理数）与数轴上的点才是一一对应关系。
因此，此说法错误。
综上所述，只有②说法是正确的。
【答案】：
A.1个。

6. 把下列各数的序号填入相应的集合内。
①$-\frac{1}{3}$；②$+8$；③20%；④$-|+5.1|$；⑤0.131 331 333 1…（相邻两个1之间3的个数逐次加1）；⑥0；⑦$\frac{\pi}{2}$；⑧$-(-1.8)$；⑨$-3$。
整数集合：{ …}；
负分数集合：{ …}；
无理数集合：{ …}。

答案： ②⑥⑨
①④
⑤⑦

7. 如图，在$4×4$的正方形网格中，按要求画出直角三角形。
（1）在图①中画一个直角三角形，使它的三边长均为有理数。
（2）在图②中画一个直角三角形，使它的一边长为有理数，另外两边长为无理数。
（3）在图③中画一个直角三角形，使它的三边长均为无理数。
]

答案：

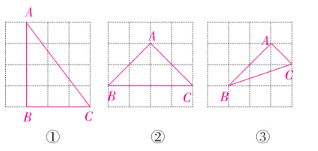
解：​
(1)​如图​①，​​△ ABC​即为所求
​
(2)​如图​②，​​ △ABC​即为所求
​
(3)​如图​③，​​ △ABC​即为所求