《2025年作业本江西教育出版社八年级数学上册北师大版》

1. 在平面直角坐标系中，若点 $ P $ 的坐标为 $ (-2025,2026) $，则点 $ P $ 在(B)

A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： B
【解析】：
题目考查了平面直角坐标系中各象限的坐标符号特点。
在平面直角坐标系中，第一象限的坐标符号为(+,+)，第二象限的坐标符号为(-,+)，第三象限的坐标符号为(-,-)，第四象限的坐标符号为(+,-)。
对于点P(-2025,2026)，其横坐标（x坐标）为负，纵坐标（y坐标）为正，所以点P位于第二象限。
【答案】：
B. 第二象限。

2. 已知点 $ A(1,2) $，过点 $ A $ 向 $ y $ 轴作垂线，垂足为 $ M $，则点 $ M $ 的坐标为(C)

A.$ (1,0) $
B.$ (2,0) $
C.$ (0,2) $
D.$ (0,-2) $

答案： C
解：过点A(1,2)向y轴作垂线，垂足M的横坐标为0，纵坐标与点A的纵坐标相同，为2，所以点M的坐标为(0,2)。
答案：C

3. 已知点 $ Q $ 的坐标为 $ (2,-3) $，点 $ P $ 的坐标为 $ (2a + 2,a - 5) $。若直线 $ PQ \perp y $ 轴，则点 $ P $ 的坐标为(D)

A.$ (2,-5) $
B.$ (2,2) $
C.$ (6,-3) $
D.$ (-14,-3) $

答案： C
解：
∵直线PQ⊥y轴，
∴点P与点Q的纵坐标相等。
∵点Q(2,-3)，点P(2a+2,a-5)，
∴a-5=-3，
解得a=2。
∴2a+2=2×2+2=6，
∴点P的坐标为(6,-3)。
答案：C

4. 若点 $ A(a,a - 1) $ 在 $ y $ 轴的左侧，则点 $ B(a^{2}+1,a) $ 在第四象限。

答案： 四
解：
∵点A(a,a-1)在y轴左侧，
∴a＜0。
∵a＜0，
∴a²+1＞0，a＜0。
∴点B(a²+1,a)的横坐标为正，纵坐标为负，
∴点B在第四象限。
第四象限

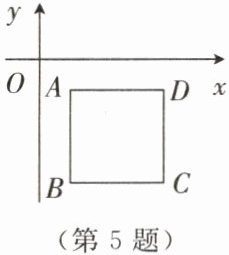
5. 如图，在平面直角坐标系中，正方形 $ ABCD $ 的边长为 3， $ AB // y $ 轴。若点 $ A $ 的坐标为 $ (1,-1) $，则点 $ B $ 的坐标为(1,-4)。
]

答案： (1，-4)
解：
∵正方形ABCD中AB//y轴，点A坐标为(1,-1)，边长为3。
∴点B与点A横坐标相同，为1。
又
∵由图可知点B在点A下方，
∴点B纵坐标为-1 - 3 = -4。
∴点B的坐标为(1,-4)。

6. 若点 $ A(a - 1,b + 2) $， $ B(3,4) $， $ C(-1,-2) $ 在同一平面直角坐标系内，且 $ AB $ 所在的直线平行于 $ x $ 轴， $ AC $ 所在的直线平行于 $ y $ 轴，则 $ a + b $ 的算术平方根为$\sqrt{2}$。

答案： $​ \sqrt 2​$
解：
∵AB所在的直线平行于x轴，
∴点A与点B的纵坐标相等，即b+2=4，解得b=2。
∵AC所在的直线平行于y轴，
∴点A与点C的横坐标相等，即a-1=-1，解得a=0。
∴a+b=0+2=2，
∴a+b的算术平方根为√2。
答案：√2

7. 已知点 $ P $ 的坐标为 $ (2m + 4,m - 1) $。
（1）若点 $ P $ 在 $ y $ 轴上，求点 $ P $ 的坐标。
（2）若点 $ P $ 在第三象限，且到两坐标轴的距离相等，求点 $ P $ 的坐标。

答案： 解：​
(1) ​依题意，得$​ 2\ \mathrm {m}+4=0​$
解得​ m=-2​
∴​m-1=-2-1=-3​
∴点​ P ​的坐标为​ (0，​​-3)​
​
(2) ​依题意，得$​ 2\ \mathrm {m}+4＜0​$
​m-1＜0，​且​ |$2\ \mathrm {m}+4$|=|m-1|​
∴​m=-5​
∴$​2\ \mathrm {m}+4=-6，$​​m-1=-6​
∴点​ P ​的坐标为​ (-6，​​-6)​

8. 在平面直角坐标系中，给出如下定义：点 $ A $ 到 $ x $ 轴、 $ y $ 轴距离的较小值称为点 $ A $ 的“短距”，当点 $ P $ 的“短距”等于点 $ Q $ 的“短距”时，称 $ P $， $ Q $ 两点为“等距点”。
(1)点 $ A(-5,2) $ 的“短距”为2。
(2)若点 $ B(-2,-2m + 1) $ 的“短距”为 1，求 $ m $ 的值。
(3)若 $ C(-1,k + 3) $， $ D(4,2k - 3) $ 两点为“等距点”，求 $ k $ 的值。

答案： 2
解：​
(2) ​依题意，得​ |$-2\ \mathrm {m}+1$|=1​
解得​ m=0 ​或​ m=1​
​
(3) ​分情况讨论：
​① ​当​ |2k-3|=1 ​时，解得​ k=1 ​或​ k=2​
当​ k=1 ​时，​k+3=4＞1，​符合题意
当​ k=2 ​时，​k+3=5＞1，​符合题意
​② ​当​ |k+3|=|2k-3| ​时，解得​ k=6 ​或​ k=0​
当​ k=0 ​时，​k+3=3＞1，​不符合题意，舍去
当​ k=6 ​时，​k+3=9＞1，​不符合题意，舍去
综上，​k ​的值为​ 1 ​或​ 2​
(1)2
(2)解：点B到x轴距离为|-2m+1|，到y轴距离为|-2|=2。
“短距”为1，分两种情况：
①|-2m+1|=1且|-2m+1|≤2
-2m+1=±1
当-2m+1=1时，m=0；当-2m+1=-1时，m=1。
验证：m=0时，|-2×0+1|=1≤2；m=1时，|-2×1+1|=1≤2，均符合。
②2=1，不成立。
综上，m=0或1。
(3)解：点C到x轴距离|k+3|，到y轴距离|-1|=1，“短距”min(|k+3|,1)；
点D到x轴距离|2k-3|，到y轴距离|4|=4，“短距”min(|2k-3|,4)。
C、D为“等距点”，分情况：
情况1：min(|k+3|,1)=min(|2k-3|,4)=1
则|k+3|≥1且|2k-3|=1
|2k-3|=1，2k-3=±1，k=2或1。
k=2时，|2+3|=5≥1；k=1时，|1+3|=4≥1，均符合。
情况2：min(|k+3|,1)=min(|2k-3|)=|k+3|（|k+3|≤1）
则|k+3|=|2k-3|且|k+3|≤1，|2k-3|≤4
|k+3|=|2k-3|，k+3=±(2k-3)
k+3=2k-3，k=6，|6+3|=9＞1，舍；
k+3=-(2k-3)，3k=0，k=0，|0+3|=3＞1，舍。
综上，k=1或2。