《2025年作业本江西教育出版社八年级数学上册北师大版》

1. 在平面直角坐标系中，点$(4,-3)$关于$x$轴对称的点的坐标是(C)

A.$(3,-4)$
B.$(-4,3)$
C.$(4,3)$
D.$(-4,-3)$

答案： C
解：关于x轴对称的点，横坐标相同，纵坐标互为相反数。
点(4,-3)关于x轴对称的点的坐标是(4,3)。
答案：C

2. 下列关于点$M(-2,5)$和点$N(2,5)$的说法中，正确的是(C)

A.关于$x$轴对称
B.与$x$轴平行
C.关于$y$轴对称
D.与$y$轴平行

答案： C
【解析】：
本题主要考察的是坐标系中点的对称性质。
首先，我们观察点M(-2,5)和点N(2,5)，可以发现这两点的纵坐标相同，即$y_1 = y_2 = 5，$而横坐标互为相反数，即$x_1 = -x_2。$
根据坐标系的性质，当两点的纵坐标相同，横坐标互为相反数时，这两点关于y轴对称。
接下来，我们逐一排除选项：
A. 关于x轴对称：这要求两点的横坐标相同，纵坐标互为相反数，与题目给出的点不符合，故A错误；
B. 与x轴平行：这要求两点的纵坐标相同，但横坐标没有特定关系，虽然本题两点的纵坐标相同，但横坐标互为相反数，更符合关于y轴对称的定义，故B错误；
C. 关于y轴对称：这要求两点的纵坐标相同，横坐标互为相反数，与题目给出的点符合，故C正确；
D. 与y轴平行：在二维坐标系中，没有与y轴平行的线段或点的说法，故D错误。
综上所述，正确答案是C。
【答案】：
C

3. 剪纸是我国民间艺术的瑰宝，很多剪纸作品展现了数学中的对称美。如图，将一幅蝴蝶剪纸放在平面直角坐标系中，如果点$E$的坐标为$(m,3)$，其关于$y$轴对称的点$F$的坐标为$(4,n)$，那么$m + n$的值为(A)

A.$-1$
B.$0$
C.$1$
D.$-9$
]

答案： A
【解析】：本题可根据关于y轴对称的点的坐标特征来求解m和n的值，进而求出m + n的值。
关于y轴对称的点的坐标特征为：纵坐标不变，横坐标互为相反数。
已知点E的坐标为(m,3)，点F的坐标为(4,n)，且点E与点F关于y轴对称。
根据上述特征可知，点E与点F的纵坐标相等，即n = 3；点E与点F的横坐标互为相反数，即m = -4。
将m = -4，n = 3代入m + n可得：m + n=-4 + 3=-1。
【答案】：A。

4. 如图，将$\triangle ABC$以$x$轴和$y$轴为对称轴依次进行两次轴对称变换后，得到$\triangle DEF$。如果点$A$，$B$，$C$的坐标分别为$A(-5,1)$，$B(-2,0)$，$C(1,3)$，那么点$D$，$E$，$F$的坐标分别为$D$(5,-1)，$E$(2,0)，$F$(-1,-3)。

答案： (5，-1)
(2，0)
(-1，-3)
【解析】：
题目考查的知识点是轴对称与坐标变化，需要用到关于x轴和y轴对称的点的坐标变化规律，关于x轴对称的点，横坐标相同，纵坐标互为相反数；关于y轴对称的点，纵坐标相同，横坐标互为相反数。
首先，$\triangle ABC$关于y轴进行轴对称变换，得到中间三角形。
对于点A(-5,1)，关于y轴对称后，横坐标变为5，纵坐标不变，得到(5,1)。
对于点B(-2,0)，关于y轴对称后，横坐标变为2，纵坐标不变，得到(2,0)。
对于点C(1,3)，关于y轴对称后，横坐标变为-1，纵坐标不变，得到(-1,3)。
然后，中间三角形再关于x轴进行轴对称变换，得到$\triangle DEF。$
对于点(5,1)，关于x轴对称后，横坐标不变，纵坐标变为-1，得到D(5,-1)。
对于点(2,0)，关于x轴对称后，横坐标不变，纵坐标仍为0，得到E(2,0)。
对于点(-1,3)，关于x轴对称后，横坐标不变，纵坐标变为-3，得到F(-1,-3)。
【答案】：
D(5,-1)；E(2,0)；F(-1,-3)。

5. 如图，在平面直角坐标系中，对$\triangle ABC$进行循环往复的轴对称变换。若原来点$A$的坐标是$(m,n)$，则经过第$2025$次变换后所得的点$A$的坐标是______。
]

答案： (m,-n)
解：由图可知，变换规律为每4次变换为一个循环。
第一次变换（关于x轴对称）：$A_1(m,-n)$
第二次变换（关于y轴对称）：$A_2(-m,-n)$
第三次变换（关于x轴对称）：$A_3(-m,n)$
第四次变换（关于y轴对称）：$A_4(m,n)，$回到初始位置。
$2025÷4=506\cdots\cdots1，$余数为1，即第2025次变换后点A的坐标与第一次变换后相同。
故答案为：(m,-n)

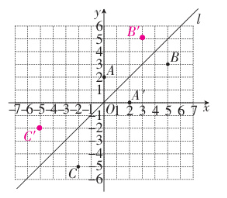
6. 如图，在平面直角坐标系中，直线$l$是第一、三象限的角平分线。
(1)已知点$A(0,2)$关于直线$l$的对称点$A'$的坐标为$(2,0)$，请在图中分别标出点$B(5,3)$，$C(-2,-5)$关于直线$l$的对称点$B'$，$C'$的位置，并写出它们的坐标：$B'$(3,5)，$C'$(-5,-2)。
(2)结合图形观察以上三组点的坐标，发现：坐标平面内任一点$P(a,b)$关于第一、三象限的角平分线$l$的对称点$P'$的坐标为(b,a)。
]

答案：
(-5，-2)
(3，5)
(b，a)