第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 如图,一棵垂直于地面的大树在台风中被折断。已知树干在离地面 $3m$ 处折断,折断后树顶端落在距离树根 $4m$ 处,则大树原来的高度为(
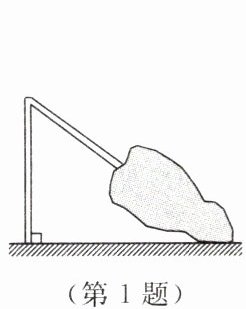
A.$5m$
B.$8m$
C.$9m$
D.$25m$
B
)
A.$5m$
B.$8m$
C.$9m$
D.$25m$
答案:
$B$
解:设树干折断处离地面部分为$ a = 3 \, m ,$树根到顶端落地点的距离为$ b = 4 \, m ,$折断部分长度为$ c 。$
由勾股定理得:$ c^2 = a^2 + b^2 $
$ c^2 = 3^2 + 4^2 = 9 + 16 = 25 $
$ c = 5 \, m ($负值舍去$)$
大树原来的高度为$ a + c = 3 + 5 = 8 \, m $
答案:$B$
解:设树干折断处离地面部分为$ a = 3 \, m ,$树根到顶端落地点的距离为$ b = 4 \, m ,$折断部分长度为$ c 。$
由勾股定理得:$ c^2 = a^2 + b^2 $
$ c^2 = 3^2 + 4^2 = 9 + 16 = 25 $
$ c = 5 \, m ($负值舍去$)$
大树原来的高度为$ a + c = 3 + 5 = 8 \, m $
答案:$B$
2. 有一道古代数学题,大意是:有一个水池,水面 $BE$ 的宽为 $16$ 尺$(1 尺 = \frac{1}{3} m)$,在水池正中央有一根芦苇,它高出水面 $2$ 尺,如果把这根芦苇垂直拉向岸边,那么它的顶端恰好到达岸边的水面,如图所示。这根芦苇的长度是(
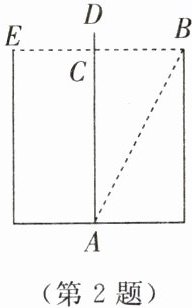
A.$26$ 尺
B.$24$ 尺
C.$17$ 尺
D.$15$ 尺
C
)
A.$26$ 尺
B.$24$ 尺
C.$17$ 尺
D.$15$ 尺
答案:
C
【解析】:本题可根据勾股定理建立方程来求解芦苇的长度。
设芦苇的长度为x尺,因为芦苇高出水面2尺,所以水深为(x - 2)尺。
已知水池水面BE的宽为16尺,那么水池一半的长度,即$BC=\frac{1}{2}×16 = 8$尺。
在由芦苇、水深和水池一半宽度构成的直角三角形中,根据勾股定理:直角三角形的两条直角边的平方和等于斜边的平方。
其中芦苇的长度为斜边,水深和水池一半宽度为两条直角边,可列出方程:$8^{2}+(x - 2)^{2}=x^{2}。$
接下来求解这个方程:
$64+x^{2}-4x + 4=x^{2}($根据完全平方公式$(a-b)^2=a^2-2ab+b^2$展开$(x - 2)^{2})$
$x^{2}-x^{2}-4x=-64 - 4($移项,将含有x的项移到等号左边,常数项移到等号右边)
-4x=-68
x = 17
【答案】:C
【解析】:本题可根据勾股定理建立方程来求解芦苇的长度。
设芦苇的长度为x尺,因为芦苇高出水面2尺,所以水深为(x - 2)尺。
已知水池水面BE的宽为16尺,那么水池一半的长度,即$BC=\frac{1}{2}×16 = 8$尺。
在由芦苇、水深和水池一半宽度构成的直角三角形中,根据勾股定理:直角三角形的两条直角边的平方和等于斜边的平方。
其中芦苇的长度为斜边,水深和水池一半宽度为两条直角边,可列出方程:$8^{2}+(x - 2)^{2}=x^{2}。$
接下来求解这个方程:
$64+x^{2}-4x + 4=x^{2}($根据完全平方公式$(a-b)^2=a^2-2ab+b^2$展开$(x - 2)^{2})$
$x^{2}-x^{2}-4x=-64 - 4($移项,将含有x的项移到等号左边,常数项移到等号右边)
-4x=-68
x = 17
【答案】:C
3. 如图,圆柱的底面周长是 $24$,高是 $5$。在圆柱下底面的点 $A$ 处有一只蚂蚁,如果它想吃到点 $B$ 处的食物,那么它沿圆柱侧面爬行的最短路程是(
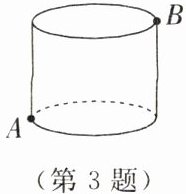
A.$9$
B.$13$
C.$14$
D.$25$
B
)
A.$9$
B.$13$
C.$14$
D.$25$
答案:
B
【解析】:
本题主要考查了勾股定理的应用以及圆柱的侧面展开图的性质。
首先,将圆柱的侧面展开,得到一个长方形。
在这个长方形中,点A和点B分别位于长方形的两侧,且它们之间的水平距离是底面周长的一半,即$\frac{24}{2}=12,$垂直距离是圆柱的高,即5。
接下来,利用勾股定理来计算点A到点B的最短距离。
根据勾股定理,直角三角形的斜边c满足:$c=\sqrt{a^2+b^2},$其中a和b是直角三角形的两条直角边。
将a=12,b=5代入公式,得到:
$c=\sqrt{12^2+5^2}=\sqrt{144+25}=\sqrt{169}=13。$
【答案】:B。
【解析】:
本题主要考查了勾股定理的应用以及圆柱的侧面展开图的性质。
首先,将圆柱的侧面展开,得到一个长方形。
在这个长方形中,点A和点B分别位于长方形的两侧,且它们之间的水平距离是底面周长的一半,即$\frac{24}{2}=12,$垂直距离是圆柱的高,即5。
接下来,利用勾股定理来计算点A到点B的最短距离。
根据勾股定理,直角三角形的斜边c满足:$c=\sqrt{a^2+b^2},$其中a和b是直角三角形的两条直角边。
将a=12,b=5代入公式,得到:
$c=\sqrt{12^2+5^2}=\sqrt{144+25}=\sqrt{169}=13。$
【答案】:B。
4. 如图,将一根长为 $8cm$ 的橡皮筋两端 $A$ 和 $B$ 固定在同一水平面上,然后把橡皮筋的中点 $C$ 垂直向上拉升 $3cm$ 到点 $D$ 的位置。橡皮筋被拉长了
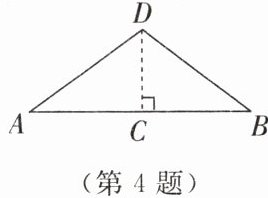
2
$cm$。
答案:
2
【解析】:
本题可根据勾股定理分别求出拉伸前后橡皮筋一半的长度,进而求出拉伸前后橡皮筋的长度,最后计算出橡皮筋被拉长的长度。
已知橡皮筋原长为8cm,因为C为AB中点,所以$AC = \frac{1}{2}AB=\frac{1}{2}×8 = 4cm。$
在直角三角形ACD中,AC = 4cm,CD = 3cm,根据勾股定理$a^2 + b^2 = c^2($其中a、b为直角边,c为斜边),可得$AD=\sqrt{AC^{2}+CD^{2}}=\sqrt{4^{2}+3^{2}}=\sqrt{16 + 9}=\sqrt{25}=5cm。$
因为AD = BD,所以拉伸后橡皮筋的长度为2AD = 2×5 = 10cm。
用拉伸后橡皮筋的长度减去原长,可得拉长的长度为10 - 8 = 2cm。
【答案】:
解:$AC = \frac{1}{2}AB=\frac{1}{2}×8 = 4cm$
在$Rt\triangle ACD$中,$AD=\sqrt{AC^{2}+CD^{2}}=\sqrt{4^{2}+3^{2}}=\sqrt{25}=5cm$
拉伸后橡皮筋的长度为2AD = 2×5 = 10cm
拉长的长度为10 - 8 = 2cm
故答案为:2。
【解析】:
本题可根据勾股定理分别求出拉伸前后橡皮筋一半的长度,进而求出拉伸前后橡皮筋的长度,最后计算出橡皮筋被拉长的长度。
已知橡皮筋原长为8cm,因为C为AB中点,所以$AC = \frac{1}{2}AB=\frac{1}{2}×8 = 4cm。$
在直角三角形ACD中,AC = 4cm,CD = 3cm,根据勾股定理$a^2 + b^2 = c^2($其中a、b为直角边,c为斜边),可得$AD=\sqrt{AC^{2}+CD^{2}}=\sqrt{4^{2}+3^{2}}=\sqrt{16 + 9}=\sqrt{25}=5cm。$
因为AD = BD,所以拉伸后橡皮筋的长度为2AD = 2×5 = 10cm。
用拉伸后橡皮筋的长度减去原长,可得拉长的长度为10 - 8 = 2cm。
【答案】:
解:$AC = \frac{1}{2}AB=\frac{1}{2}×8 = 4cm$
在$Rt\triangle ACD$中,$AD=\sqrt{AC^{2}+CD^{2}}=\sqrt{4^{2}+3^{2}}=\sqrt{25}=5cm$
拉伸后橡皮筋的长度为2AD = 2×5 = 10cm
拉长的长度为10 - 8 = 2cm
故答案为:2。
5. 木工制作一个长方形桌面,测得桌面的长为 $60cm$,宽为 $32cm$,对角线长为 $68cm$。这个桌面
合格
(填“合格”或“不合格”)。
答案:
合格
【解析】:
本题考察的是勾股定理的应用。在直角三角形中,直角边的平方和等于斜边的平方。对于长方形桌面,其对角线、长和宽应满足勾股定理。
设桌面的长为a,宽为b,对角线为c,则应满足$a^2 + b^2 = c^2。$
将题目中给出的数据代入公式,即$60^2 + 32^2 $是否等于$ 68^2,$进行计算以验证桌面是否合格。
【答案】:
计算得:
$60^2 + 32^2 = 3600 + 1024 = 4624$
$68^2 = 4624$
由于$ 60^2 + 32^2 = 68^2,$根据勾股定理的逆定理,这个桌面的角度是直角,因此,这个桌面合格。
故答案为:合格。
【解析】:
本题考察的是勾股定理的应用。在直角三角形中,直角边的平方和等于斜边的平方。对于长方形桌面,其对角线、长和宽应满足勾股定理。
设桌面的长为a,宽为b,对角线为c,则应满足$a^2 + b^2 = c^2。$
将题目中给出的数据代入公式,即$60^2 + 32^2 $是否等于$ 68^2,$进行计算以验证桌面是否合格。
【答案】:
计算得:
$60^2 + 32^2 = 3600 + 1024 = 4624$
$68^2 = 4624$
由于$ 60^2 + 32^2 = 68^2,$根据勾股定理的逆定理,这个桌面的角度是直角,因此,这个桌面合格。
故答案为:合格。
6. 如图,在 $\triangle ABC$ 中,$AC = 8$,$BC = 6$,$CE$ 是 $AB$ 边上的中线,$CD$ 是 $AB$ 边上的高,且 $AE = 5$,求 $CD$ 的长。
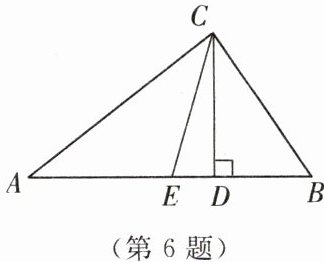

答案:
解:
∵CE 是 AB 边上的中线
∴AE=BE=5
∴AB=10
又
∵AC=8,BC=6
∴$AC^2+BC^2=8^2+6^2=100=AB^2$
∴△ABC 是直角三角形
又
∵CD 是△ ABC 的高
∴$S_{△ABC}=\frac 12\ \mathrm {A}C·BC=\frac 12\ \mathrm {A}B·CD$
∴$CD=\frac {AC·BC}{AB}=\frac {8×6}{10}=4.8$
∵CE 是 AB 边上的中线
∴AE=BE=5
∴AB=10
又
∵AC=8,BC=6
∴$AC^2+BC^2=8^2+6^2=100=AB^2$
∴△ABC 是直角三角形
又
∵CD 是△ ABC 的高
∴$S_{△ABC}=\frac 12\ \mathrm {A}C·BC=\frac 12\ \mathrm {A}B·CD$
∴$CD=\frac {AC·BC}{AB}=\frac {8×6}{10}=4.8$
查看更多完整答案,请扫码查看


