第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 下列计算正确的是(
A.$\sqrt{3} + \sqrt{3} = 3$
B.$4\sqrt{5} - \sqrt{5} = 4$
C.$\sqrt{3}×\sqrt{2} = \sqrt{6}$
D.$\sqrt{32}÷\sqrt{8} = 4$
C
)A.$\sqrt{3} + \sqrt{3} = 3$
B.$4\sqrt{5} - \sqrt{5} = 4$
C.$\sqrt{3}×\sqrt{2} = \sqrt{6}$
D.$\sqrt{32}÷\sqrt{8} = 4$
答案:
C
解:$A.\sqrt{3} + \sqrt{3} = 2\sqrt{3} \neq 3,$故A错误;
$B.4\sqrt{5} - \sqrt{5} = 3\sqrt{5} \neq 4,$故B错误;
$C.\sqrt{3} × \sqrt{2} = \sqrt{3×2} = \sqrt{6},$故C正确;
$D.\sqrt{32} ÷ \sqrt{8} = \sqrt{32÷8} = \sqrt{4} = 2 \neq 4,$故D错误。
结论:C
解:$A.\sqrt{3} + \sqrt{3} = 2\sqrt{3} \neq 3,$故A错误;
$B.4\sqrt{5} - \sqrt{5} = 3\sqrt{5} \neq 4,$故B错误;
$C.\sqrt{3} × \sqrt{2} = \sqrt{3×2} = \sqrt{6},$故C正确;
$D.\sqrt{32} ÷ \sqrt{8} = \sqrt{32÷8} = \sqrt{4} = 2 \neq 4,$故D错误。
结论:C
2. 下列计算正确的是(
A.$\sqrt{3}÷\frac{1}{\sqrt{6}} = 2\sqrt{3}$
B.$\sqrt{12} = 2\sqrt{3}$
C.$(2\sqrt{3})^{2} = 6$
D.$\sqrt{2} + \sqrt{3} = \sqrt{5}$
B
)A.$\sqrt{3}÷\frac{1}{\sqrt{6}} = 2\sqrt{3}$
B.$\sqrt{12} = 2\sqrt{3}$
C.$(2\sqrt{3})^{2} = 6$
D.$\sqrt{2} + \sqrt{3} = \sqrt{5}$
答案:
B
解:
$A. \sqrt{3} ÷ \frac{1}{\sqrt{6}} = \sqrt{3}×\sqrt{6} = \sqrt{18} = 3\sqrt{2} ≠ 2\sqrt{3},$错误。
$B. \sqrt{12} = \sqrt{4×3} = 2\sqrt{3},$正确。
$C. (2\sqrt{3})^{2} = 2^2×(\sqrt{3})^2 = 4×3 = 12 ≠ 6,$错误。
$D. \sqrt{2}$与$\sqrt{3}$不是同类二次根式,不能合并,错误。
结论:B
解:
$A. \sqrt{3} ÷ \frac{1}{\sqrt{6}} = \sqrt{3}×\sqrt{6} = \sqrt{18} = 3\sqrt{2} ≠ 2\sqrt{3},$错误。
$B. \sqrt{12} = \sqrt{4×3} = 2\sqrt{3},$正确。
$C. (2\sqrt{3})^{2} = 2^2×(\sqrt{3})^2 = 4×3 = 12 ≠ 6,$错误。
$D. \sqrt{2}$与$\sqrt{3}$不是同类二次根式,不能合并,错误。
结论:B
3. 如图,在正方形$ABCD$中,若正方形$AEPF$和正方形$PHCG$的面积分别为$12$和$3$,则正方形$ABCD$的边长为(
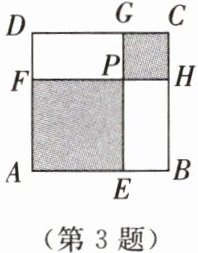
A.$9$
B.$15$
C.$2\sqrt{2}$
D.$3\sqrt{3}$
D
)
A.$9$
B.$15$
C.$2\sqrt{2}$
D.$3\sqrt{3}$
答案:
D
解:
∵正方形AEPF的面积为12,
∴其边长AE = √12 = 2√3。
∵正方形PHCG的面积为3,
∴其边长PH = √3。
由图可知,正方形ABCD的边长AB = AE + EB,且EB = PH = √3,
∴AB = 2√3 + √3 = 3√3。
答案:D。
解:
∵正方形AEPF的面积为12,
∴其边长AE = √12 = 2√3。
∵正方形PHCG的面积为3,
∴其边长PH = √3。
由图可知,正方形ABCD的边长AB = AE + EB,且EB = PH = √3,
∴AB = 2√3 + √3 = 3√3。
答案:D。
4. 已知一个长方形的长为$2\sqrt{3} + \sqrt{2}$,宽为$\sqrt{12} - \sqrt{2}$。
(1)该长方形的周长为
(2)该长方形的面积为
(1)该长方形的周长为
$8\sqrt{3}$
。(2)该长方形的面积为
$10$
。
答案:
$ 8\sqrt 3$
10
(1)解:长方形周长=2×(长+宽)
=2×[(2√3 + √2)+(√12 - √2)]
=2×(2√3 + √2 + 2√3 - √2)
=2×4√3
=8√3
(2)解:长方形面积=长×宽
=(2√3 + √2)(√12 - √2)
=(2√3 + √2)(2√3 - √2)
=(2√3)² - (√2)²
=12 - 2
=10
10
(1)解:长方形周长=2×(长+宽)
=2×[(2√3 + √2)+(√12 - √2)]
=2×(2√3 + √2 + 2√3 - √2)
=2×4√3
=8√3
(2)解:长方形面积=长×宽
=(2√3 + √2)(√12 - √2)
=(2√3 + √2)(2√3 - √2)
=(2√3)² - (√2)²
=12 - 2
=10
5. 计算。
(1)$2×(1 - \sqrt{2}) + \sqrt{8}$;
(2)$(4\sqrt{3} + 3\sqrt{6})÷2\sqrt{3}$;
(3)$\frac{1}{2}\sqrt{32} - 2\sqrt{75} + \sqrt{0.5} - 3\sqrt{\frac{1}{27}}$。
(1)$2×(1 - \sqrt{2}) + \sqrt{8}$;
(2)$(4\sqrt{3} + 3\sqrt{6})÷2\sqrt{3}$;
(3)$\frac{1}{2}\sqrt{32} - 2\sqrt{75} + \sqrt{0.5} - 3\sqrt{\frac{1}{27}}$。
答案:
$ =2-2\sqrt 2+2\sqrt 2$
=2
$=4\sqrt 3÷2\sqrt 3+2\sqrt 6÷2\sqrt 3$
$= 2 + \frac {3\sqrt {2}}{2}$
$=2\sqrt 2-10\sqrt 3+\frac {\sqrt 2}2-\frac {\sqrt 3}3$
$= \frac {5\sqrt {2}}{2} - \frac {31\sqrt {3}}{3}$
=2
$=4\sqrt 3÷2\sqrt 3+2\sqrt 6÷2\sqrt 3$
$= 2 + \frac {3\sqrt {2}}{2}$
$=2\sqrt 2-10\sqrt 3+\frac {\sqrt 2}2-\frac {\sqrt 3}3$
$= \frac {5\sqrt {2}}{2} - \frac {31\sqrt {3}}{3}$
6. 计算:$(2\sqrt{5} - 3\sqrt{2})(2\sqrt{5} + 3\sqrt{2}) - (\sqrt{6} - \sqrt{3})^{2}$。
答案:
解:原式
$ =(2\sqrt{5} - 3\sqrt{2})(2\sqrt{5} + 3\sqrt{2}) - (\sqrt{6} - \sqrt{3})^{2}$
$ =(2\sqrt{5})^{2} - (3\sqrt{2})^{2} - [(\sqrt{6})^{2} - 2\times\sqrt{6}\times\sqrt{3} + (\sqrt{3})^{2}]$
$ =20 - 18 - (6 - 2\sqrt{18} + 3)$
$ =2 - (9 - 6\sqrt{2})$
$ =2 - 9 + 6\sqrt{2}$
$ =6\sqrt{2} - 7$
$ =(2\sqrt{5} - 3\sqrt{2})(2\sqrt{5} + 3\sqrt{2}) - (\sqrt{6} - \sqrt{3})^{2}$
$ =(2\sqrt{5})^{2} - (3\sqrt{2})^{2} - [(\sqrt{6})^{2} - 2\times\sqrt{6}\times\sqrt{3} + (\sqrt{3})^{2}]$
$ =20 - 18 - (6 - 2\sqrt{18} + 3)$
$ =2 - (9 - 6\sqrt{2})$
$ =2 - 9 + 6\sqrt{2}$
$ =6\sqrt{2} - 7$
7. 已知$x = \sqrt{3} + \sqrt{2}$,$y = \sqrt{3} - \sqrt{2}$。
(1)求$xy$的值。
(2)求$x^{2} + 3xy + y^{2}$的值。
(1)求$xy$的值。
(2)求$x^{2} + 3xy + y^{2}$的值。
答案:
解:$(1) xy=(\sqrt 3+\sqrt 2)(\sqrt 3-\sqrt 2)$
=3-2=1
$(2) x^2+3xy+y^2$
$=(x^2+2xy+y^2)+xy$
$=(x+y)^2+xy$
$=(\sqrt 3+\sqrt 2+\sqrt 3-\sqrt 2)^2+1$
=12+1
=13
=3-2=1
$(2) x^2+3xy+y^2$
$=(x^2+2xy+y^2)+xy$
$=(x+y)^2+xy$
$=(\sqrt 3+\sqrt 2+\sqrt 3-\sqrt 2)^2+1$
=12+1
=13
查看更多完整答案,请扫码查看


