《2025年作业本江西教育出版社八年级数学上册北师大版》

7. 小明对A和B两家网约车公司各10名司机的月收入进行了抽样调查，结果如图所示。

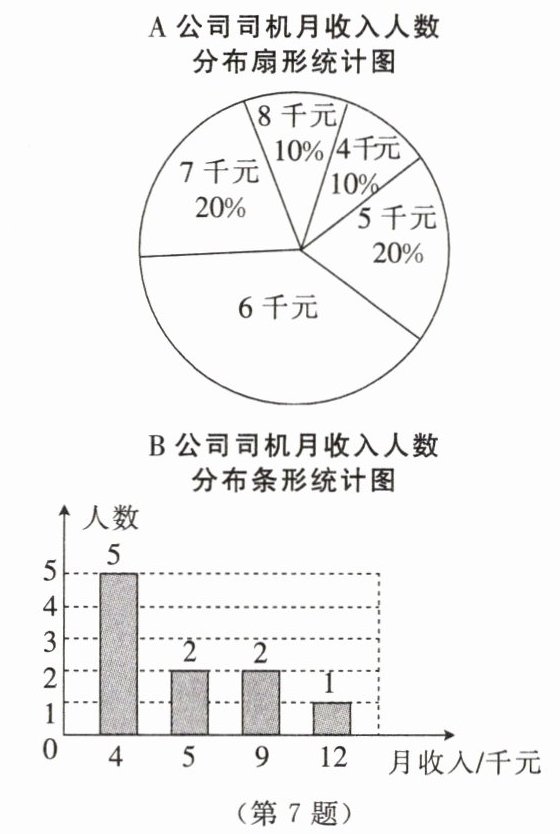
根据以上信息，解答下列问题。
（1）完成表格：

（2）小明的叔叔计划从这两家公司中选择一家做网约车司机，如果你是小明，你会建议他选哪家公司？请说明理由。

答案： （1）6
7.6
（2）解：选 A，理由如下：
两家公司各 10 名司机的月收入平均数相同，
但 A 公司司机月收入的众数大于 B 公司，
且方差较小，更稳定。

8. 王老师统计了6名同学的数学成绩（单位：分）：55，57，64，65，67，69。他决定按照“组内离差平方和达到最小”的方法，将以上6名同学分成两个学习互助小组。请你帮助王老师完成分组，并说明理由。（平均数保留小数点后两位）

答案：
解：将​$6$​个数据按从小到大的顺序排序并分组，
共有​$5$​种情况
​$①\{55\}，$​{​$57，$​​$64，$​​$65，$​​$67，$​​$69$​}；
​$②$​{​$55，$​​$57$​}，{​$64，$​​$65，$​​$67，$​​$69$​}；
​$③$​{​$55，$​​$57，$​​$64$​}，{​$65，$​​$67，$​​$69$​}；
​$④$​{​$55，$​​$57，$​​$64，$​​$65$​}，{​$67，$​​$69$​}；
​$⑤$​{​$55，$​​$57，$​​$64，$​​$65，$​​$67$​}，​$\{69\}。$​
以第​$2$​种分组情况为例，计算组内离差平方和
其中，第一组有​$2$​个数据​$55，$​​$57，$​这​$2$​个数据的
平均数是​$56，$​故第二组数据的组内离差平方和
​$S_{1}^2=(55-56)^2+(57-56)^2=2；$​
第二组有​$4$​个数据​$64，$​​$65，$​​$67，$​​$69，$​
这​$4$​个数据的平均数是​$66.25，$​故第二组数据的
组内离差平方和​$S_{2}^2=(64-66.25)^2+(65-66.25)^2$​
​$+(67-66.25)^2+(69-66.25)^2=14.75$​
因此，第​$2$​种分组情况的组内离差平方和
​$S_{2}^2=S_{1}^2+S_{2}^2=2+14.75=16.75$​
同理计算其他​$4$​种分组情况的组内离差平方和
结果如下

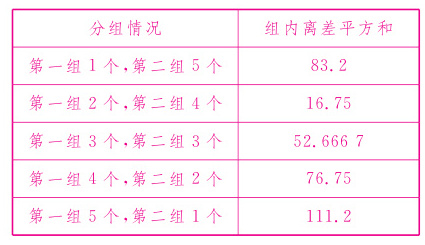
计算结果表明，第​$2$​种情况的组内离差平方和最小
因此把​$6$​名同学按成绩分成的两组
是​$55，$​​$57，$​​$64，$​​$65，$​​$67，$​​$69。$​