《2025年作业本江西教育出版社八年级数学上册北师大版》

1. 有下列函数：① $ y = 5x $；② $ y = - 2x - 1 $；③ $ y = \frac{2}{x} $；④ $ y = \frac{1}{2}x - 6 $；⑤ $ y = x^{2} - 1 $。其中是一次函数的有①②④$ $，是正比例函数的有①$ $。（均填序号）

答案： ①②④
①
【解析】：
本题考查了一次函数和正比例函数的定义。
一次函数的一般形式为 y = kx + b，其中 k 和 b 是常数，且$ k \neq 0。$
正比例函数是特殊的一次函数，其形式为 y = kx，其中 k 是常数且$ k \neq 0。$
对于给定的函数：
① y = 5x：这是正比例函数，因为它可以写成 y = kx 的形式，其中 k = 5。
同时，它也是一次函数，因为它也可以写成 y = kx + b 的形式，其中 k = 5, b = 0。
② y = -2x - 1：这是一次函数，因为它可以写成 y = kx + b 的形式，其中 k = -2, b = -1。
$③ y = \frac{2}{x}$：这不是一次函数，因为 x 的指数不为 1。
$④ y = \frac{1}{2}x - 6$：这是一次函数，因为它可以写成 y = kx + b 的形式，其中$ k = \frac{1}{2}, b = -6。$
$⑤ y = x^2 - 1$：这不是一次函数，因为 x 的最高次数为 2。
【答案】：
是一次函数的有：①②④；
是正比例函数的有：①。

2. 若 $ y = (a - 3)x + a^{2} - 9 $ 为正比例函数，则 $ a $ 的值为-3$ $。

答案： -3
【解析】：
题目要求$y = (a-3)x + a^2 - 9$为正比例函数。
正比例函数的一般形式为y = kx，其中k为非零常数。
因此，我们需要使$y = (a-3)x + a^2 - 9$满足正比例函数的形式。
首先，我们比较系数，得到以下两个条件：
$a - 3 \neq 0，$确保x的系数不为零。
$a^2 - 9 = 0，$确保常数项为零。
解第二个方程$a^2 - 9 = 0，$我们得到：
(a - 3)(a + 3) = 0
$a = 3 \quad $或$ \quad a = -3$
但由于第一个条件$a - 3 \neq 0，$所以a不能等于3。
因此，a = -3。
【答案】：
a = -3

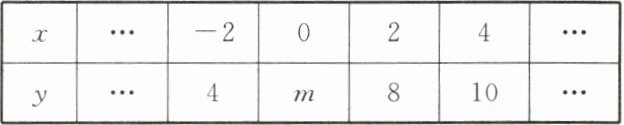
3. 在一次函数 $ y = kx + b $ 中，$ x $，$ y $ 的几组对应值如下表所示。根据表中数据可以得到 $ m =$6$$ $ $，$ k =$1$$ $ $。

答案： 6
1
【解析】：本题可根据一次函数y = kx + b中，当x = 0时，y=b，先求出m的值，再利用待定系数法求出k的值。
步骤一：求m的值
在一次函数y = kx + b中，当x = 0时，y=b，即函数图象与y轴交点的纵坐标为b。
已知当x = 0时，y = m，所以m就是函数y = kx + b中b的值。
观察表格可知，当x = 2时，y = 8；当x = 4时，y = 10。
因为一次函数是单调函数，且4-2=10 - 8 = 2，即x每增加2，y增加2。
那么当x从0增加到2时，x增加了2，所以y也应增加2，已知x = 2时y = 8，则x = 0时y=m = 6。
步骤二：求k的值
已知m = 6，即当x = 0时，y = 6，所以b = 6，则一次函数的表达式为y = kx + 6。
把x = 2，y = 8代入y = kx + 6中，可得8 = 2k + 6。
求解上述方程：
8 = 2k + 6
移项可得2k=8 - 6，即2k = 2。
两边同时除以2，解得k = 1。
【答案】：m = 6；k = 1。

4. 如图①，$ AD $ 是 $ \triangle ABC $ 的边 $ BC $ 上的高，且 $ AD = 8 \mathrm{~cm} $，$ BC = 9 \mathrm{~cm} $。点 $ E $ 从点 $ B $ 出发，沿线段 $ BC $ 向终点 $ C $ 运动，其速度 $ v $（单位：$ \mathrm{cm} / \mathrm{s} $）与时间 $ x $（单位：$ \mathrm{s} $）的关系如图②所示。设 $ \triangle ABE $ 的面积为 $ y $（单位：$ \mathrm{cm}^{2} $）。
（1）点 $ E $ 的运动速度是3$ \mathrm{cm} / \mathrm{s} $。
（2）$ y $ 与 $ x $ 的关系式为y=12x$ $。
（3）$ x $ 每增加 $ 1 \mathrm{~s} $，$ y $ 的变化情况是y增加12cm²$ $。
（4）当 $ y = 30 \mathrm{~cm}^{2} $ 时，$ x $ 的值是2.5$ $。
]

答案： 3
$y = 12x(0\leq x\leq3)$
y 增加$ 12\ \text{cm}^2$
$\frac{5}{2}$

5. 将长为 $ 40 \mathrm{~cm} $、宽为 $ 15 \mathrm{~cm} $ 的长方形白纸按下图所示的方式黏合起来，得到一个大长方形，黏合部分的宽为 $ 5 \mathrm{~cm} $。

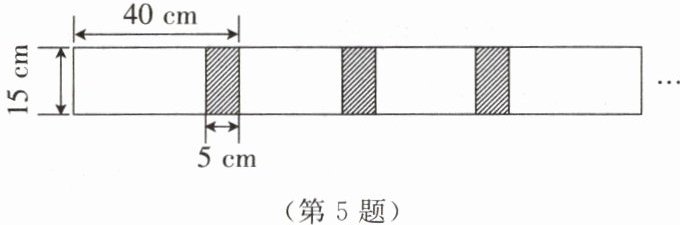
（1）根据上图，将表格补充完整。

（2）设 $ x $ 张白纸黏合后得到的大长方形的长为 $ y \mathrm{~cm} $，写出 $ y $ 与 $ x $ 之间的关系式。
（3）当 $ x = 20 $ 时，求 $ y $ 的值。白纸黏合起来的总长度可能为 $ 2020 \mathrm{~cm} $ 吗？为什么？
（4）设 $ x $ 张白纸黏合后得到的大长方形的面积为 $ S \mathrm{~cm}^{2} $，写出 $ S $ 与 $ x $ 之间的关系式，并求出当 $ x = 3 $ 时 $ S $ 的值。

答案： 75
180
解：​
(2) y=40+35(x-1)=35x+5​
​
(3) ​当​ x=20 ​时，​y=705​
不可能。理由如下：
依题意，得​ 2020=35x+5​
解得$​ x=\frac {403}7​$
因为​ x ​必须为整数，所以不可能
​
(4) ​依题意，得​S=15(35x+5)=525x+75​
当​ x=3 ​时，​S=525×3+75=1650​