《2025年作业本江西教育出版社八年级数学上册北师大版》

1. 某班7名同学已学会烹饪的菜品种数依次为3，5，4，6，3，3，4，这组数据的众数、中位数和平均数分别是(A)

A.3，4，4
B.4，3，4
C.3，3，4
D.4，4，3

答案： A
【解析】：
本题主要考查众数、中位数和平均数的定义及计算方法。
众数是一组数据中出现次数最多的数。
中位数是将一组数据从小到大（或从大到小）排列后，位于中间的数。
如果数据量为奇数，则中位数是中间的那个数；如果数据量为偶数，则中位数是中间两个数的平均值。
平均数是所有数据的和除以数据的数量。
首先，我们找出这组数据的众数。
数据为3,5,4,6,3,3,4，其中数字3出现了3次，而其他数字出现的次数都少于3次。
因此，众数是3。
接着，我们找出中位数。
首先将数据从小到大排列：3, 3, 3, 4, 4, 5, 6。
因为数据量是7（奇数），所以中位数就是排列后的第4个数，即4。
最后，我们计算平均数。
平均数是所有数据的和除以数据的数量，即(3+5+4+6+3+3+4) ÷ 7 = 28 ÷ 7 = 4。
综上所述，众数是3，中位数是4，平均数是4。
【答案】：A

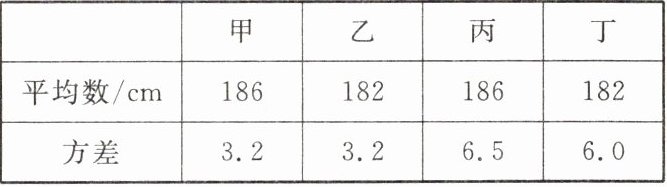
2. 下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差。现要从中选择一名成绩优异且发挥稳定的运动员参赛，应该选择(A)


A.甲
B.乙
C.丙
D.丁

答案： A
【解析】：本题考查平均数和方差的意义。
平均数用于反映数据的平均水平，而方差用于衡量数据的波动大小，即稳定性。
首先，比较四名运动员的平均成绩：
甲的平均成绩为186cm，
乙的平均成绩为182cm，
丙的平均成绩为186cm，
丁的平均成绩为182cm。
从平均成绩来看，甲和丙的平均成绩较高，都是186cm，而乙和丁的平均成绩较低，都是182cm。因此，可以初步判断甲和丙的成绩更优异。
接下来，比较甲和丙的方差：
甲的方差为3.2，
丙的方差为6.5。
方差越小，表示数据波动越小，即发挥越稳定。因此，甲的方差更小，说明甲的发挥更稳定。
综上所述，甲的平均成绩高且方差小，即成绩优异且发挥稳定。
【答案】：A

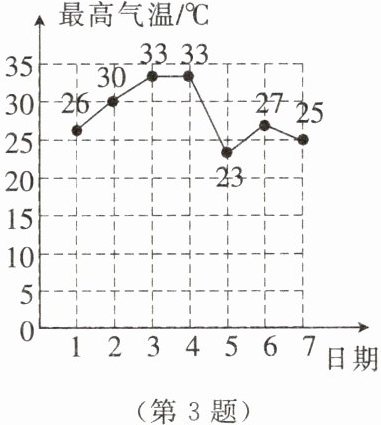
3. 某市5月1日至7日的日最高气温如图所示。下列说法错误的是(D)

A.5月4日至5日的日最高气温下降幅度最大
B.众数是33℃
C.平均数是$\frac{197}{7}$℃
D.中位数是33℃

答案： D
【解析】：本题主要考查了折线统计图的应用，以及众数、平均数和中位数的计算。
A选项：从折线统计图中可以看出，5月4日至5日的日最高气温从$33^{\circ}C$下降到了$23^{\circ}C，$下降幅度为$10^{\circ}C，$是相邻两天中下降幅度最大的，所以A选项正确。
B选项：众数是一组数据中出现次数最多的数。从折线统计图中可以看出，$33^{\circ}C$出现了2次，是出现次数最多的数，所以众数是$33^{\circ}C，$B选项正确。
C选项：平均数是所有数据的和除以数据的个数。
平均数$ = \frac{26 + 30 + 33 + 33 + 23 + 27 + 25}{7} = \frac{197}{7}^{\circ}C，$
所以C选项正确。
D选项：中位数是将一组数据从小到大（或从大到小）排列后，位于中间位置的数。
将数据从小到大排列得：23, 25, 26, 27, 30, 33, 33，
因为数据有7个，所以中位数是第4个数，即$27^{\circ}C，$与D选项中的$33^{\circ}C$不符，所以D选项错误。
【答案】：D。

4. 若一组数据3，5，9，10，12，$x$的中位数和众数相等，则这组数据的平均数是8。

答案： 8
【解析】：
本题考查中位数、众数及平均数的概念及计算方法。
首先，需要根据中位数和众数的定义，分别考虑x可能的取值。
中位数是将一组数据从小到大排序后，位于中间的数。
如果数据量为奇数，则中位数是中间那个数；
如果数据量为偶数，则中位数是中间两个数的平均值。
众数是一组数据中出现次数最多的数。
题目中数据组有6个数（包括x），是偶数个数，需要找到中间两个数来计算中位数。
同时，需要考虑众数的可能情况，并使得中位数和众数相等。
当$x \leq 5$时，数据排序后为x, 3, 5, 9, 10, 12。
中位数为$\frac{5+9}{2}=7，$但众数不可能为7（因为没有其他数与7相等），所以这种情况不符合题意。
当5 ＜ x ＜ 9时，数据排序后中间的两个数会变化，但中位数不会是整数（因为不是两个相同的数相加后除以2），而众数需要是整数，所以这种情况也不符合题意。
当x = 9时，数据排序后为3, 5, 9, 9, 10, 12。
中位数为$\frac{9+9}{2}=9，$众数也为9（因为9出现的次数最多），符合题意。
此时，平均数为$\frac{3+5+9+9+10+12}{6}=8。$
当9 ＜ x ＜ 10时，同样中位数不会是整数，众数也需要是整数，所以这种情况不符合题意。
当$x \geq 10$时，数据排序后中间的两个数会包括10，但此时众数不可能与中位数相等（除非所有数都相同，但题目中已有其他不同的数），所以这种情况也不符合题意。
综上所述，只有当x=9时，中位数和众数相等，且都为9。
此时，这组数据的平均数为8。
【答案】：
8

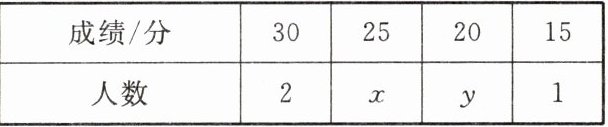
5. 某班10名同学的中考体育测试成绩统计如下表所示。若成绩的平均数是23，众数是$a$，中位数是$b$，则$a - b$的值是-2.5。

答案： -2.5
解：由题意得，总人数为10，即2 + x + y + 1 = 10，则x + y = 7。
平均数是23，可得$\frac{30×2 + 25x + 20y + 15×1}{10} = 23，$化简得60 + 25x + 20y + 15 = 230，即25x + 20y = 155，两边同时除以5得5x + 4y = 31。
联立方程组$\begin{cases}x + y = 7 \\ 5x + 4y = 31\end{cases}，$解得x = 3，y = 4。
成绩分布为：15（1人），20（4人），25（3人），30（2人）。
众数a = 20，中位数$b = \frac{20 + 25}{2} = 22.5。$
a - b = 20 - 22.5 = -2.5
答案：-2.5

6. 嘉嘉在计算一组数据的方差时，列出的算式为$s^{2}=\frac{1}{10}[3(8-\overline{x})^{2}+2(7-\overline{x})^{2}+m(5-\overline{x})^{2}+(9-\overline{x})^{2}]$。请分析算式中的信息，判断这组数据的众数为。

答案： 5
【解析】：
首先，我们观察给出的方差算式：
$s^{2} = \frac{1}{10}[3(8-\overline{x})^{2} + 2(7-\overline{x})^{2} + m(5-\overline{x})^{2} + (9-\overline{x})^{2}]$
其中，每个数据点与平均数的差的平方都乘以了一个系数，这些系数代表了该数据点出现的次数。
从算式中，我们可以看到：
数字8的系数为3，表示8出现了3次；
数字7的系数为2，表示7出现了2次；
数字5的系数为m，表示5出现了m次；
数字9的系数为1，表示9出现了1次。
由于总的数据个数是10（由$\frac{1}{10}$可知），并且这些数据的总和应该是10个数据点，所以有：
3 + 2 + m + 1 = 10
解得：m = 4
这意味着数字5出现了4次，是出现次数最多的数字。
【答案】：
众数为5。

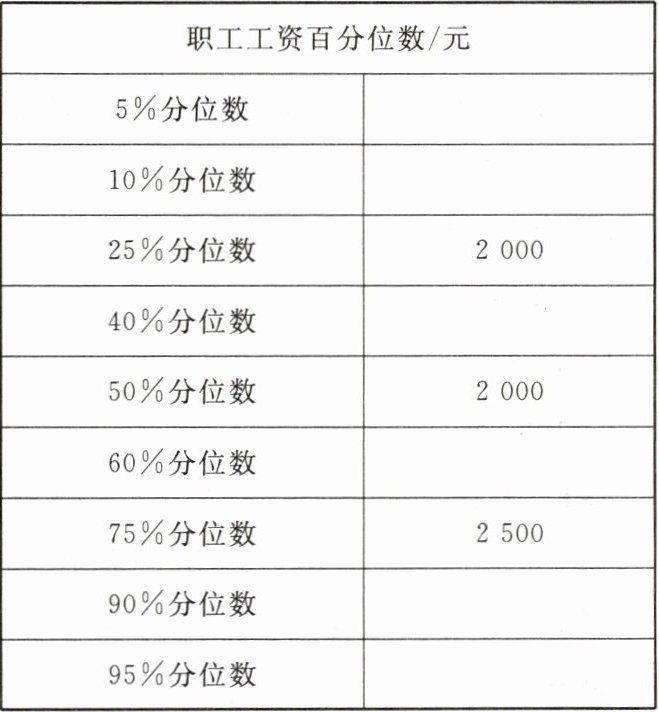
7. 某公司全体职工的月工资情况统计如下表所示：

(1)该公司的普通职工最关注的数据是()
A. 中位数和众数
B. 平均数和众数
C. 平均数和中位数
D. 平均数和方差
(2)填写下面的表格。

(3)完成该公司职工工资百分位数值表。

答案： （1）A
（2）2000
2000
2000
2500
（3）1200
1500
2000
2500
6000
8000