《2025年作业本江西教育出版社八年级数学上册北师大版》

10. 在平面直角坐标系中，若 $ A(a,3) $，$ B(-2,b) $ 两点关于 x 轴对称，则 ab 的值是6。

答案： 6
【解析】：
本题主要考查平面直角坐标系中关于x轴对称的点的坐标性质。
在平面直角坐标系中，如果两点关于x轴对称，那么它们的横坐标相同，纵坐标互为相反数。
根据题目条件，点A(a,3)和点B(-2,b)关于x轴对称，因此可以得出：
a = -2 （横坐标相同）
b = -3 （纵坐标互为相反数）
接下来，我们需要求出ab的值。
【答案】：
ab = (-2) × (-3) = 6
故答案为：6。

11. 已知直线 $ y = kx - 4 $ 与直线 $ y = 2x $ 平行，若直线 $ y = kx - 4 $ 经过点 $ (a,-2) $，则 $ a = $1。

答案： 1
解：因为直线y=kx - 4与直线y=2x平行，所以k=2，则直线为y=2x - 4。
又因为直线y=2x - 4经过点(a, - 2)，所以将点代入得：-2 = 2a - 4，解得2a=2，a=1。
1

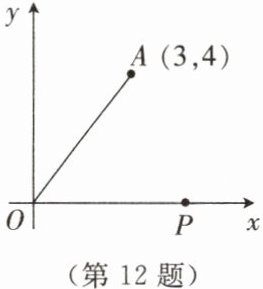
12. 如图，在平面直角坐标系中，点 A 的坐标为 $ (3,4) $，点 P 在 x 轴正半轴上。若以点 P，O，A 为顶点的三角形是等腰三角形，则满足条件的点 P 的坐标为(5,0),(6,0),$(\frac{25}{6},0)$。

答案： ​ (5，​​0)，​​(6，​​0)，$​​(\frac {25}{6}，$​​0)​
解：
∵点A(3,4)，O(0,0)，
∴OA=√(3²+4²)=5。
设点P(m,0)(m＞0)。
情况1：OA=OP时，OP=5，
∴m=5，点P(5,0)。
情况2：OA=AP时，AP=5，
√[(m-3)²+(0-4)²]=5，
(m-3)²+16=25，
(m-3)²=9，
m-3=±3，m=6或m=0(舍)，点P(6,0)。
情况3：OP=AP时，m=√[(m-3)²+16]，
m²=(m-3)²+16，
m²=m²-6m+9+16，
6m=25，m=25/6，点P(25/6,0)。
综上，点P的坐标为(5,0)，(6,0)，(25/6,0)。

13. 计算。
（1）$ \sqrt[3]{-8} + (\sqrt{2} - 1)^{0} - \sqrt{9} $；
（2）$ 3\sqrt{24} + \sqrt{\frac{3}{2}} - \sqrt{3}(\sqrt{2} - \sqrt{3}) + (\sqrt{6} - 3)^{2} $。

答案：
(1) 解：原式=-2 + 1 - 3
=-4
(2) 解：原式$=3×2\sqrt{6} + \frac{\sqrt{6}}{2} - \sqrt{6} + 3 + 6 - 6\sqrt{6} + 9$
$=6\sqrt{6} + \frac{\sqrt{6}}{2} - \sqrt{6} + 3 + 6 - 6\sqrt{6} + 9$
$=(6\sqrt{6} - 6\sqrt{6}) + (\frac{\sqrt{6}}{2} - \sqrt{6}) + (3 + 6 + 9)$
$=-\frac{\sqrt{6}}{2} + 18$

14. 某校数学兴趣小组来到操场上测量旗杆 AB 的高度。小华测得从旗杆顶端垂下的升旗用的绳子比旗杆长 2 m，如图①所示。小明拉着绳子的下端往后退，当绳子拉直时，小华测得此时小明拉绳子的手到地面的距离 CD 为 1 m，到旗杆的距离 CE 为 9 m，如图②所示。求旗杆的高度 AB。

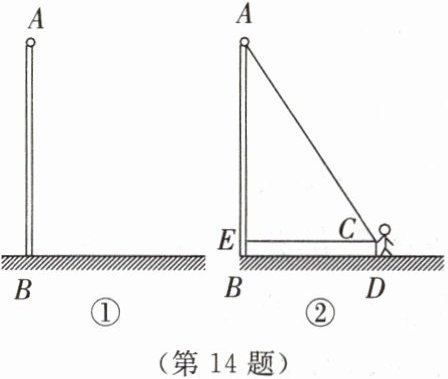
答案： 解：设​ AB ​的长为$​ x\ \mathrm {m}，$​则绳子的长
为$​ (x+2)\ \mathrm {m}，$​​AE ​的长为$​ (x-1)\ \mathrm {m}​$
在​ Rt △ACE ​中，$​AC=(x+2)\ \mathrm {m}，$​
$​AE=(x-1)\ \mathrm {m}，$$​​CE=9\ \mathrm {m}​$
由勾股定理，得$​ (x-1)^2+9^2=(x+2)^2​$
解得​ x=13​
答：旗杆的高度​ AB ​为$​ 13\ \mathrm {m}。$​

15. 如图，正方形网格中每个小正方形的边长都是 1，每个小正方形的顶点叫作格点，以格点为顶点分别按下列要求作图。
（1）在图①中画一个三角形，使三角形的三边长分别为 $ \sqrt{26} $，$ 3\sqrt{2} $，$ 2\sqrt{5} $。
（2）在图②中画一个面积为 4 的等腰直角三角形。

答案：

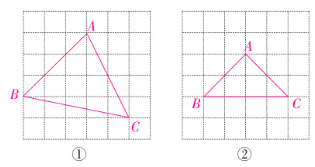
解：如图所示