第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 为了解甲、乙两种甜玉米的产量情况,农科院各用10块自然条件相同的试验田进行试验,测得各试验田每公顷的产量,并绘制成如图所示的统计图。下列判断正确的是(
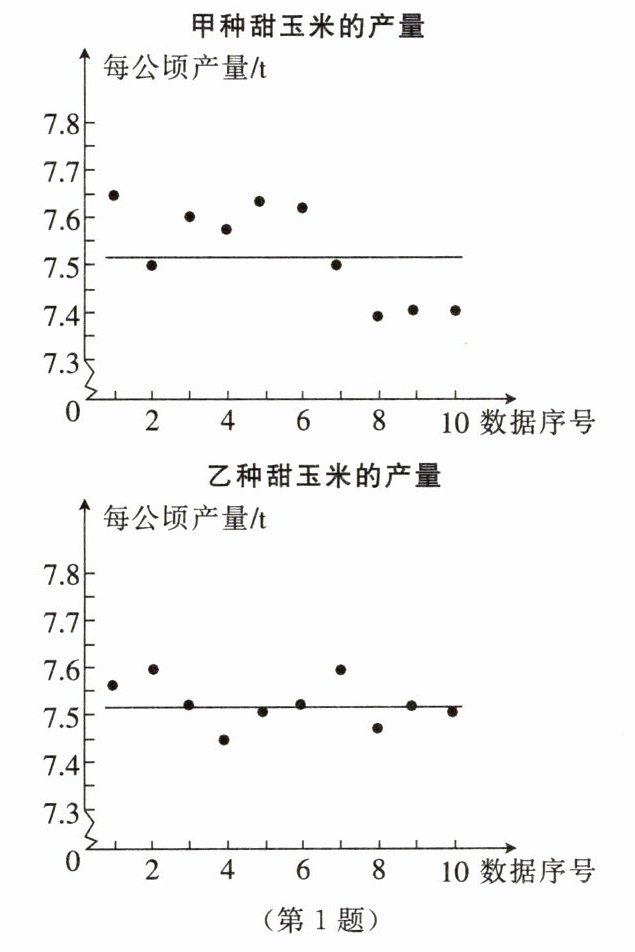
A.甲种甜玉米平均产量大
B.乙种甜玉米平均产量大
C.甲种甜玉米产量波动大
D.乙种甜玉米产量波动大
C
)
A.甲种甜玉米平均产量大
B.乙种甜玉米平均产量大
C.甲种甜玉米产量波动大
D.乙种甜玉米产量波动大
答案:
$C$
解:$ $
$1. $计算甲种甜玉米平均产量$ $
甲产量数据$($单位:$t)$:$7.6, 7.5, 7.6, 7.6, 7.6, 7.5, 7.4, 7.4, 7.4 $
$($注:根据统计图读取$10$个数据,修正后应为:$7.6, 7.5, 7.6, 7.6, 7.6, 7.5, 7.4, 7.4, 7.4, 7.4) $
甲$ = \frac{7.6+7.5+7.6+7.6+7.6+7.5+7.4+7.4+7.4+7.4}{10} = 7.5 $
$2. $计算乙种甜玉米平均产量$ $
乙产量数据$($单位:$t)$:$7.5, 7.6, 7.5, 7.4, 7.5, 7.5, 7.6, 7.4, 7.5, 7.5 $
乙$ = \frac{7.5+7.6+7.5+7.4+7.5+7.5+7.6+7.4+7.5+7.5}{10} = 7.5 $
$3. $比较波动大小$ $
甲数据分布范围:$7.4~7.6,$乙数据分布范围:$7.4~7.6。$$ $
甲数据中$7.4$和$7.6$的频数更高,偏离平均数更集中;乙数据更集中于$7.5,$波动更小。$ $
$($或通过观察统计图,甲数据点分布更分散$) $
结论:甲种甜玉米产量波动大。$ $
答案:$C$
解:$ $
$1. $计算甲种甜玉米平均产量$ $
甲产量数据$($单位:$t)$:$7.6, 7.5, 7.6, 7.6, 7.6, 7.5, 7.4, 7.4, 7.4 $
$($注:根据统计图读取$10$个数据,修正后应为:$7.6, 7.5, 7.6, 7.6, 7.6, 7.5, 7.4, 7.4, 7.4, 7.4) $
甲$ = \frac{7.6+7.5+7.6+7.6+7.6+7.5+7.4+7.4+7.4+7.4}{10} = 7.5 $
$2. $计算乙种甜玉米平均产量$ $
乙产量数据$($单位:$t)$:$7.5, 7.6, 7.5, 7.4, 7.5, 7.5, 7.6, 7.4, 7.5, 7.5 $
乙$ = \frac{7.5+7.6+7.5+7.4+7.5+7.5+7.6+7.4+7.5+7.5}{10} = 7.5 $
$3. $比较波动大小$ $
甲数据分布范围:$7.4~7.6,$乙数据分布范围:$7.4~7.6。$$ $
甲数据中$7.4$和$7.6$的频数更高,偏离平均数更集中;乙数据更集中于$7.5,$波动更小。$ $
$($或通过观察统计图,甲数据点分布更分散$) $
结论:甲种甜玉米产量波动大。$ $
答案:$C$
2. 运动会200 m赛跑中,5名运动员的成绩如下表所示,其中有两个数据被墨迹污染了,这两个数据依次是(

A.30,4
B.30,2
C.32,4
D.32,2
B
)
A.30,4
B.30,2
C.32,4
D.32,2
答案:
B
【解析】:本题考查了平均数和标准差的知识点。
首先,我们根据平均成绩的定义来找出被污染的成绩。
平均成绩是所有成绩之和除以成绩的数量,即:
平均成绩$ = \frac{所有成绩之和}{成绩的数量},$
题目中给出平均成绩为33s,成绩的数量为5,
我们可以设被污染的成绩为x,
那么所有成绩之和就是32 + 34 + x + 36 + 33。
将这些值代入平均成绩的定义中,我们得到:
$33 = \frac{32 + 34 + x + 36 + 33}{5},$
解这个方程,我们可以找到x的值:
33 × 5 = 32 + 34 + x + 36 + 33,
165 = 135 + x,
x = 30,
接下来,我们需要计算标准差来验证选项。
标准差是衡量数据离散程度的统计量,它的计算公式是:
标准差$ = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_i - \mu)^2},$
其中N是数据的数量,x_i是每个数据点,$\mu$是平均数。
将已知的数据和计算出的x值代入标准差的公式中,我们可以得到:
标准差$ = \sqrt{\frac{1}{5}\left[(32-33)^2 + (34-33)^2 + (30-33)^2 + (36-33)^2 + (33-33)^2\right]},$
标准差$ = \sqrt{\frac{1}{5}\left[1 + 1 + 9 + 9 + 0\right]},$
标准差$ = \sqrt{\frac{20}{5}},$
标准差 = 2,
综上所述,被污染的两个数据依次是30和2,所以正确答案是B。
【答案】:B。
【解析】:本题考查了平均数和标准差的知识点。
首先,我们根据平均成绩的定义来找出被污染的成绩。
平均成绩是所有成绩之和除以成绩的数量,即:
平均成绩$ = \frac{所有成绩之和}{成绩的数量},$
题目中给出平均成绩为33s,成绩的数量为5,
我们可以设被污染的成绩为x,
那么所有成绩之和就是32 + 34 + x + 36 + 33。
将这些值代入平均成绩的定义中,我们得到:
$33 = \frac{32 + 34 + x + 36 + 33}{5},$
解这个方程,我们可以找到x的值:
33 × 5 = 32 + 34 + x + 36 + 33,
165 = 135 + x,
x = 30,
接下来,我们需要计算标准差来验证选项。
标准差是衡量数据离散程度的统计量,它的计算公式是:
标准差$ = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_i - \mu)^2},$
其中N是数据的数量,x_i是每个数据点,$\mu$是平均数。
将已知的数据和计算出的x值代入标准差的公式中,我们可以得到:
标准差$ = \sqrt{\frac{1}{5}\left[(32-33)^2 + (34-33)^2 + (30-33)^2 + (36-33)^2 + (33-33)^2\right]},$
标准差$ = \sqrt{\frac{1}{5}\left[1 + 1 + 9 + 9 + 0\right]},$
标准差$ = \sqrt{\frac{20}{5}},$
标准差 = 2,
综上所述,被污染的两个数据依次是30和2,所以正确答案是B。
【答案】:B。
3. 某校国旗护卫队原来有5名学生,身高(单位:cm)分别为173,174,174,174,175。若增加一名身高为174的学生,则国旗护卫队学生身高的方差会
变小
(填“变大”,“变小”或“不变”)。
答案:
变小
解:原数据平均数:$\frac{173 + 174 + 174 + 174 + 175}{5} = 174$
原方差:$\frac{(173 - 174)^2 + 3×(174 - 174)^2 + (175 - 174)^2}{5} = \frac{1 + 0 + 1}{5} = 0.4$
新数据平均数:$\frac{173 + 174×4 + 175}{6} = 174$
新方差:$\frac{(173 - 174)^2 + 4×(174 - 174)^2 + (175 - 174)^2}{6} = \frac{1 + 0 + 1}{6} ≈ 0.33$
因为0.33 < 0.4,所以方差变小。
变小
解:原数据平均数:$\frac{173 + 174 + 174 + 174 + 175}{5} = 174$
原方差:$\frac{(173 - 174)^2 + 3×(174 - 174)^2 + (175 - 174)^2}{5} = \frac{1 + 0 + 1}{5} = 0.4$
新数据平均数:$\frac{173 + 174×4 + 175}{6} = 174$
新方差:$\frac{(173 - 174)^2 + 4×(174 - 174)^2 + (175 - 174)^2}{6} = \frac{1 + 0 + 1}{6} ≈ 0.33$
因为0.33 < 0.4,所以方差变小。
变小
4. 若一组数据$x_{1}$,$x_{2}$,…,$x_{n}$的平均数为5,方差为16,则另一组数据$3x_{1}+2$,$3x_{2}+2$,…,$3x_{n}+2$的标准差为
12
。
答案:
12
【解析】:
本题主要考察平均数与方差的性质以及标准差的计算。
首先,已知一组数据$x_1,x_2,…,x_n$的平均数为5,方差为16。
对于另一组数据$3x_1+2,3x_2+2,…,3x_n+2,$其平均数为原平均数乘以3再加2,即3 × 5 + 2 = 17。
其方差为原方差乘以3的平方,即$3^2 × 16 = 144。$
标准差是方差的平方根,所以新数据的标准差为$\sqrt{144} = 12。$
【答案】:
12
【解析】:
本题主要考察平均数与方差的性质以及标准差的计算。
首先,已知一组数据$x_1,x_2,…,x_n$的平均数为5,方差为16。
对于另一组数据$3x_1+2,3x_2+2,…,3x_n+2,$其平均数为原平均数乘以3再加2,即3 × 5 + 2 = 17。
其方差为原方差乘以3的平方,即$3^2 × 16 = 144。$
标准差是方差的平方根,所以新数据的标准差为$\sqrt{144} = 12。$
【答案】:
12
5. 若一组数据4,a,5,6,b的平均数为5,众数为5,则这组数据的方差为
0.4
。
答案:
0.4
解:
∵ 数据4,a,5,6,b的平均数为5
∴ (4+a+5+6+b)/5 = 5
解得:a+b=10
∵ 众数为5
∴ a,b中至少有一个为5
分两种情况:
① 若a=5,则b=10-5=5,数据为4,5,5,6,5
② 若b=5,则a=10-5=5,数据为4,5,5,6,5
两种情况数据相同,均为4,5,5,5,6
计算方差:
$\bar{x}=5 $
$s^2=\frac{1}{5}[(4-5)^2+(5-5)^2+(5-5)^2+(5-5)^2+(6-5)^2]=\frac{1}{5}[1+0+0+0+1]=\frac{2}{5}=0.4 $
答案:0.4
解:
∵ 数据4,a,5,6,b的平均数为5
∴ (4+a+5+6+b)/5 = 5
解得:a+b=10
∵ 众数为5
∴ a,b中至少有一个为5
分两种情况:
① 若a=5,则b=10-5=5,数据为4,5,5,6,5
② 若b=5,则a=10-5=5,数据为4,5,5,6,5
两种情况数据相同,均为4,5,5,5,6
计算方差:
$\bar{x}=5 $
$s^2=\frac{1}{5}[(4-5)^2+(5-5)^2+(5-5)^2+(5-5)^2+(6-5)^2]=\frac{1}{5}[1+0+0+0+1]=\frac{2}{5}=0.4 $
答案:0.4
6. 某图书馆管理员统计了社会科学和自然科学这两类图书近5天的借阅情况,其中社会科学类图书近5天的借阅本数依次为40,46,46,40,43,自然科学类图书近5天借阅本数的方差为3.2。请计算并说明,这两类图书中,哪一类图书近5天的借阅情况较稳定。
答案:
解:社会科学类图书近5天借阅本数的平均数
为$\frac 15×(40+46+46+40+43)=43$
方差为$\frac 15×[2×(40-43)^2+2×(46-43)^2$
$+(43-43)^2]=7.2$
∵3.2<7.2
∴自然科学类图书近5天的借阅情况较稳定
为$\frac 15×(40+46+46+40+43)=43$
方差为$\frac 15×[2×(40-43)^2+2×(46-43)^2$
$+(43-43)^2]=7.2$
∵3.2<7.2
∴自然科学类图书近5天的借阅情况较稳定
查看更多完整答案,请扫码查看


