第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 若点$(-1,y_{1})$,$(2,y_{2})$在一次函数$y=(k - 2)x + b$的图象上,且$y_{1} > y_{2}$,则下列$k$的取值符合条件的是(
A.$k = 1$
B.$k = 2$
C.$k = 3$
D.$k = 4$
A
)A.$k = 1$
B.$k = 2$
C.$k = 3$
D.$k = 4$
答案:
A
【解析】:
题目考查了一次函数的单调性,即当斜率大于0时,函数是增函数;当斜率小于0时,函数是减函数。
由于$ (-1, y_1) $和$ (2, y_2) $在函数 y = (k-2)x + b 的图象上,且$ y_1 > y_2,$
根据一次函数的性质,当 x 的值从 -1 增加到 2,如果 y 的值减小,则斜率 k-2 必须小于0。
即需要满足条件 k - 2 < 0,
解得k < 2。
检查选项发现只有A选项满足该条件。
【答案】:A
【解析】:
题目考查了一次函数的单调性,即当斜率大于0时,函数是增函数;当斜率小于0时,函数是减函数。
由于$ (-1, y_1) $和$ (2, y_2) $在函数 y = (k-2)x + b 的图象上,且$ y_1 > y_2,$
根据一次函数的性质,当 x 的值从 -1 增加到 2,如果 y 的值减小,则斜率 k-2 必须小于0。
即需要满足条件 k - 2 < 0,
解得k < 2。
检查选项发现只有A选项满足该条件。
【答案】:A
2. 在同一平面直角坐标系中,函数$y = ax$和$y = -ax + a$的图象可能是(
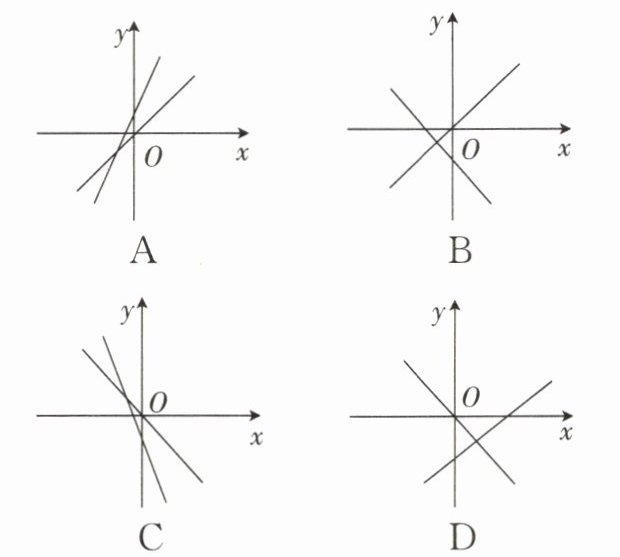
D
)
答案:
D
解:分两种情况讨论:
情况一:当 a > 0 时,
函数 y = ax 的图象经过第一、三象限,且 y 随 x 的增大而增大;
函数 y = -ax + a 中,-a < 0,a > 0,所以图象经过第一、二、四象限,且 y 随 x 的增大而减小。
情况二:当 a < 0 时,
函数 y = ax 的图象经过第二、四象限,且 y 随 x 的增大而减小;
函数 y = -ax + a 中,-a > 0,a < 0,所以图象经过第一、三、四象限,且 y 随 x 的增大而增大。
观察各选项,只有选项 D 符合上述情况。
答案:D
解:分两种情况讨论:
情况一:当 a > 0 时,
函数 y = ax 的图象经过第一、三象限,且 y 随 x 的增大而增大;
函数 y = -ax + a 中,-a < 0,a > 0,所以图象经过第一、二、四象限,且 y 随 x 的增大而减小。
情况二:当 a < 0 时,
函数 y = ax 的图象经过第二、四象限,且 y 随 x 的增大而减小;
函数 y = -ax + a 中,-a > 0,a < 0,所以图象经过第一、三、四象限,且 y 随 x 的增大而增大。
观察各选项,只有选项 D 符合上述情况。
答案:D
3. 如图,在平面直角坐标系中,点$A$,$B$都在直线$y = -2x + m$($m$为常数)上。若点$A$,$B$的横坐标分别为$-1$和$2$,$AC// y$轴,$BC// x$轴,则$\triangle ABC$的面积为(
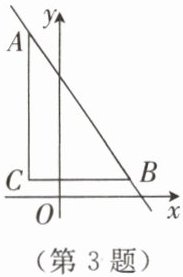
A.$6$
B.$9$
C.$12$
D.与$m$有关
B
)
A.$6$
B.$9$
C.$12$
D.与$m$有关
答案:
B
解:
∵点A、B在直线y=-2x+m上,
点A横坐标为-1,代入得y_A=-2×(-1)+m=2+m,
∴A(-1, 2+m);
点B横坐标为2,代入得y_B=-2×2+m=-4+m,
∴B(2, -4+m)。
∵AC//y轴,
∴点C横坐标与A相同,为-1;
∵BC//x轴,
∴点C纵坐标与B相同,为-4+m;
∴C(-1, -4+m)。
AC=|(2+m)-(-4+m)|=6,
BC=|2-(-1)|=3,
$S_{\triangle ABC}=\frac{1}{2}×AC×BC=\frac{1}{2}×6×3=9。$
答案:B
解:
∵点A、B在直线y=-2x+m上,
点A横坐标为-1,代入得y_A=-2×(-1)+m=2+m,
∴A(-1, 2+m);
点B横坐标为2,代入得y_B=-2×2+m=-4+m,
∴B(2, -4+m)。
∵AC//y轴,
∴点C横坐标与A相同,为-1;
∵BC//x轴,
∴点C纵坐标与B相同,为-4+m;
∴C(-1, -4+m)。
AC=|(2+m)-(-4+m)|=6,
BC=|2-(-1)|=3,
$S_{\triangle ABC}=\frac{1}{2}×AC×BC=\frac{1}{2}×6×3=9。$
答案:B
4. 若一次函数$y = kx - 1$($k\neq 0$)的函数值$y$随$x$的增大而减小,则它的图象不经过第
一
象限。
答案:
一
解:因为一次函数$y = kx - 1(k \neq 0)$的函数值y随x的增大而减小,所以k < 0。
在一次函数y = kx + b中,b = -1 < 0。
当k < 0,b < 0时,函数图象经过第二、三、四象限,不经过第一象限。
解:因为一次函数$y = kx - 1(k \neq 0)$的函数值y随x的增大而减小,所以k < 0。
在一次函数y = kx + b中,b = -1 < 0。
当k < 0,b < 0时,函数图象经过第二、三、四象限,不经过第一象限。
5. 我国古代建筑中广泛应用的榫卯结构通过凹凸结合实现木构件的紧密连接,如图所示。已知一个木构件的长度为$6$,其凸出部分的长为$1$。若将$x$个相同的木构件紧密拼接成一列,其总长度为$y$,则$y$关于$x$的关系式可表示为
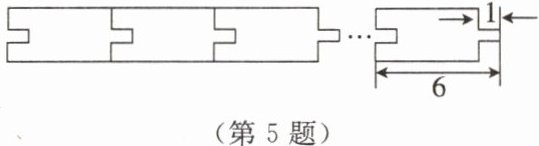
y = 5x + 1
。
答案:
y = 5x + 1
解:当拼接1个木构件时,总长度为6;
当拼接2个木构件时,重叠部分长度为1,总长度为6 + 6 - 1 = 6×2 - 1;
当拼接3个木构件时,重叠部分长度为1×2,总长度为6×3 - 1×2;
……
当拼接x个木构件时,重叠部分有(x - 1)处,每处长度为1,总长度y = 6x - 1×(x - 1) = 5x + 1。
故答案为:y = 5x + 1
解:当拼接1个木构件时,总长度为6;
当拼接2个木构件时,重叠部分长度为1,总长度为6 + 6 - 1 = 6×2 - 1;
当拼接3个木构件时,重叠部分长度为1×2,总长度为6×3 - 1×2;
……
当拼接x个木构件时,重叠部分有(x - 1)处,每处长度为1,总长度y = 6x - 1×(x - 1) = 5x + 1。
故答案为:y = 5x + 1
6. 如图,直线$y = -\dfrac{3}{4}x + 3$与$y$轴、$x$轴分别交于点$A$,$B$,点$C$在直线$AB$上,点$C$的横坐标为$1$。
(1)求点$A$,$B$,$C$的坐标。
(2)求$\triangle BOC$的面积。
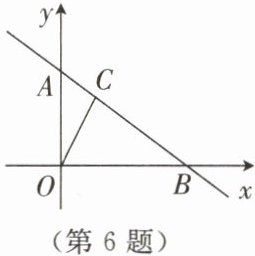
(1)求点$A$,$B$,$C$的坐标。
(2)求$\triangle BOC$的面积。

答案:
解:
(1)
∵直线$ y=-\frac 34x+3 $与 y 轴、
x 轴分别交于点 A,B
当 x=0 时,y=3
当 y=0 时,$-\frac 34x+3=0,$解得 x=4
∴点 A 的坐标为 (0,3),点 B 的坐标为 (4,0)
当 x=1 时,$y=-\frac 34+3=\frac 94$
∴点 C 的坐标为 (1,$\frac 94)$
(2)
∵点 B 的坐标为 (4,0),
∴OB=4
∵点 C 的坐标为 (1,$\frac 94)$
∴$S_{△BOC}=\frac 12×\frac 94×4=\frac 92$
【解析】:本题主要考查一次函数图象上点的坐标特征以及三角形面积的计算。
(1)对于直线$y = -\frac{3}{4}x + 3,$
当x = 0时,y = 3,所以点A的坐标为(0,3);
当y = 0时,$-\frac{3}{4}x + 3 = 0,$解得x = 4,所以点B的坐标为(4,0)。
因为点C在直线AB上,且点C的横坐标为1,将x = 1代入$y = -\frac{3}{4}x + 3,$得$y = -\frac{3}{4} + 3=\frac{9}{4},$所以点C的坐标为$(1,\frac{9}{4})。$
(2)在$\triangle BOC$中,以OB为底边,C点纵坐标的绝对值为高。
由(1)知OB = 4,C点纵坐标为$\frac{9}{4},$根据三角形面积公式$S = \frac{1}{2}×$底×高,可得${S}_{\triangle BOC}=\frac{1}{2}× OB×\vert {y}_{C}\vert=\frac{1}{2}× 4×\frac{9}{4}=\frac{9}{2}。$
(1)
∵直线$ y=-\frac 34x+3 $与 y 轴、
x 轴分别交于点 A,B
当 x=0 时,y=3
当 y=0 时,$-\frac 34x+3=0,$解得 x=4
∴点 A 的坐标为 (0,3),点 B 的坐标为 (4,0)
当 x=1 时,$y=-\frac 34+3=\frac 94$
∴点 C 的坐标为 (1,$\frac 94)$
(2)
∵点 B 的坐标为 (4,0),
∴OB=4
∵点 C 的坐标为 (1,$\frac 94)$
∴$S_{△BOC}=\frac 12×\frac 94×4=\frac 92$
【解析】:本题主要考查一次函数图象上点的坐标特征以及三角形面积的计算。
(1)对于直线$y = -\frac{3}{4}x + 3,$
当x = 0时,y = 3,所以点A的坐标为(0,3);
当y = 0时,$-\frac{3}{4}x + 3 = 0,$解得x = 4,所以点B的坐标为(4,0)。
因为点C在直线AB上,且点C的横坐标为1,将x = 1代入$y = -\frac{3}{4}x + 3,$得$y = -\frac{3}{4} + 3=\frac{9}{4},$所以点C的坐标为$(1,\frac{9}{4})。$
(2)在$\triangle BOC$中,以OB为底边,C点纵坐标的绝对值为高。
由(1)知OB = 4,C点纵坐标为$\frac{9}{4},$根据三角形面积公式$S = \frac{1}{2}×$底×高,可得${S}_{\triangle BOC}=\frac{1}{2}× OB×\vert {y}_{C}\vert=\frac{1}{2}× 4×\frac{9}{4}=\frac{9}{2}。$
查看更多完整答案,请扫码查看


