《2025年作业本江西教育出版社八年级数学上册北师大版》

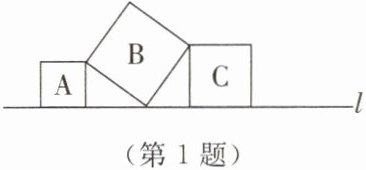
1. 如图，直线 $ l $ 上有三个正方形 $ \mathrm{A},\mathrm{B},\mathrm{C} $。若正方形 $ \mathrm{A},\mathrm{C} $ 的面积分别为 $ 5 $ 和 $ 11 $，则正方形 $ \mathrm{B} $ 的边长为(D)

A.$ 55 $
B.$ 16 $
C.$ 6 $
D.$ 4 $

答案： D
【解析】：本题可根据正方形的面积公式以及勾股定理来求解正方形B的面积，进而得到其边长。
设正方形A、B、C的边长分别为a、b、c。
根据正方形面积公式S = 边长×边长，已知正方形A的面积为5，则$a^{2}=5；$正方形C的面积为11，则$c^{2}=11。$
观察图形可知，三个正方形拼成一个直角三角形，其中正方形A和C的边长分别为直角三角形的两条直角边，正方形B的边长为斜边。
根据勾股定理：在任何一个直角三角形中，两条直角边长的平方和等于斜边长的平方，可得$a^{2}+c^{2}=b^{2}。$
将$a^{2}=5，$$c^{2}=11$代入$a^{2}+c^{2}=b^{2}，$可得$b^{2}=5 + 11 = 16。$
因为正方形的面积$S = b^{2}，$所以正方形B的面积为16，那么正方形B的边长为$\sqrt{16}=4。$
【答案】：D

2. 在 $ \triangle ABC $ 中，$ \angle A,\angle B,\angle C $ 的对边分别为 $ a,b,c $。下列条件不能判定 $ \triangle ABC $ 为直角三角形的是(D)

A.$ \angle A+\angle B=\angle C $
B.$ \angle A:\angle B:\angle C=1:2:3 $
C.$ a^{2}=c^{2}-b^{2} $
D.$ a:b:c=3:4:6 $

答案： D
解：
A.
∵∠A+∠B+∠C=180°，∠A+∠B=∠C，
∴2∠C=180°，∠C=90°，能判定直角三角形。
B. 设∠A=x，∠B=2x，∠C=3x，
∵x+2x+3x=180°，6x=180°，x=30°，
∴∠C=3x=90°，能判定直角三角形。
C.
∵a²=c²-b²，
∴a²+b²=c²，能判定直角三角形。
D. 设a=3k，b=4k，c=6k，
∵(3k)²+(4k)²=9k²+16k²=25k²，(6k)²=36k²，25k²≠36k²，
∴不能判定直角三角形。
结论：D

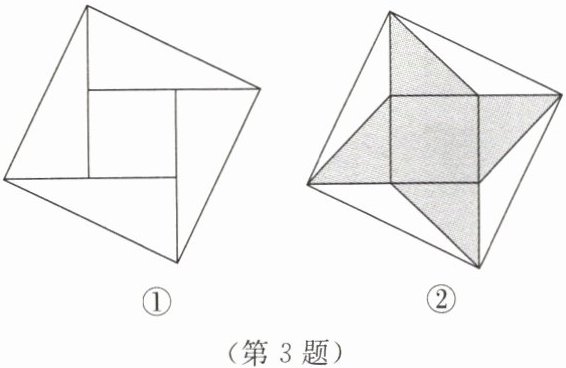
3. 如图，四个全等的直角三角形围成一个大正方形，中间是个小正方形，人们称它为“赵爽弦图”。连接四条线段得到图②所示的新的图案。如果图①中的直角三角形的长直角边为 $ 9 $，短直角边为 $ 4 $，图②中阴影部分的面积为 $ S $，那么 $ S $ 的值为(C)

A.$ 56 $
B.$ 60 $
C.$ 65 $
D.$ 75 $

答案： C

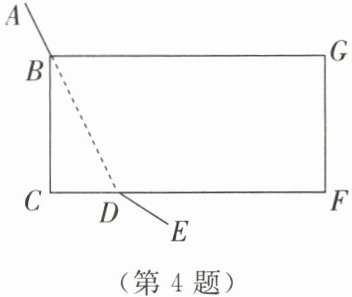
4. 如图，长方形 $ BCFG $ 是一块草地，折线 $ ABCDE $ 是一条人行道，其中 $ BC=15\,\mathrm{m},CD=8\,\mathrm{m} $。为了避免行人穿过草地(走虚线 $ BD $)，践踏绿草，管理部门分别在 $ B,D $ 处各挂了一块布告牌，牌上写着“少走6米，踏之何忍”。

答案： 6
解：由题意知，四边形BCFG是长方形，所以BC=FG=15m，CF=BG，且∠BCD=90°。
在Rt△BCD中，BC=15m，CD=8m，根据勾股定理可得：
BD = √(BC² + CD²) = √(15² + 8²) = √(225 + 64) = √289 = 17(m)
原人行道折线BCDE的长度为BC + CD = 15 + 8 = 23(m)
走虚线BD比原人行道少走的距离为23 - 17 = 6(m)
故答案为6。

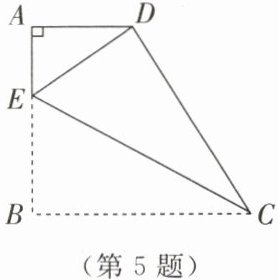
5. 如图，在四边形 $ ABCD $ 中，$ \angle A=90^{\circ} $，$ AB=4\,\mathrm{cm},AD=2\,\mathrm{cm},BC=CD $，$ E $ 是 $ AB $ 上一点。若将四边形 $ ABCD $ 沿 $ CE $ 折叠，恰好使 $ B,D $ 两点重合，则 $ DE= $2.5cm。

答案： 2.5cm
解：设 AE = x \, cm ，则 BE = (4 - x) \, cm 。
由折叠性质得： DE = BE = (4 - x) \, cm 。
在$ Rt\triangle ADE $中，$ \angle A = 90° ，$ AD = 2 \, cm ，
根据勾股定理：$ AE^2 + AD^2 = DE^2 ，$
即$ x^2 + 2^2 = (4 - x)^2 ，$
展开得$ x^2 + 4 = 16 - 8x + x^2 ，$
化简得 8x = 12 ，解得 x = 1.5 。
DE = 4 - x = 4 - 1.5 = 2.5 \, cm 。
2.5

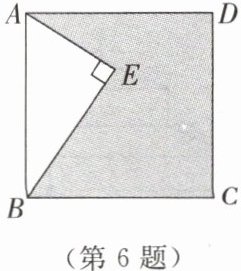
6. 如图，四边形 $ ABCD $ 是正方形，$ AE\perp BE $ 于点 $ E $。若 $ AE=3,BE=4 $，则阴影部分的面积是19。

答案： 19
【解析】：本题考查了勾股定理以及正方形面积的计算。
首先利用勾股定理计算出AB的长度。
然后通过正方形面积公式计算出正方形的面积。
最后用正方形面积减去三角形ABE的面积即可得到阴影部分的面积。
【答案】：解：
∵$ AE \perp BE $
∴△ABE为直角三角形
∵ AE= 3,BE= 4
∴$ AB^2=AE^2+BE^2=3^2+4^2=25 $
∴ AB=5
∵四边形 ABCD 是正方形
∴正方形 ABCD的面积为：$AB^2=25$
∵ AE= 3,BE= 4
∴△ABE的面积为：$\frac{1}{2} × 4× 3=6$
∴阴影部分的面积为：25-6=19
故答案为19。