《2025年作业本江西教育出版社八年级数学上册北师大版》

10. 我国南宋数学家秦九韶在《数书九章》中提出了著名的“三斜求积”公式，即如果一个三角形三条边的长度分别为$a$，$b$，$c$，那么该三角形的面积$S=\sqrt{\frac{1}{4}[a^2b^2-(\frac{a^2 + b^2 - c^2}{2})^2]}$。若$\triangle ABC$的三边长分别为$2$，$\sqrt{6}$，$3$，则$\triangle ABC$的面积为$\frac{\sqrt{95}}{4}$。

答案： $\frac{\sqrt{95}}{4}$
【解析】：
本题主要考察秦九韶的“三斜求积”公式的应用。
首先，将给定的三边长$a=2, b=\sqrt{6}, c=3$代入秦九韶的“三斜求积”公式中：
$S = \sqrt{\frac{1}{4}[a^2b^2 - (\frac{a^2 + b^2 - c^2}{2})^2]}$
代入后得到：
$S = \sqrt{\frac{1}{4} × \left[ 2^2 × (\sqrt{6})^2 - \left( \frac{2^2 + (\sqrt{6})^2 - 3^2}{2} \right)^2 \right]}$
接下来，我们按照运算的优先级进行计算：
1. 计算$ a^2, b^2, c^2$：
$a^2 = 4, \quad b^2 = 6, \quad c^2 = 9$
2. 计算$ a^2b^2 $和$ \frac{a^2 + b^2 - c^2}{2}$：
$a^2b^2 = 4 × 6 = 24$
$\frac{a^2 + b^2 - c^2}{2} = \frac{4 + 6 - 9}{2} = \frac{1}{2}$
3. 计算$ \left( \frac{a^2 + b^2 - c^2}{2} \right)^2$：
$\left( \frac{1}{2} \right)^2 = \frac{1}{4}$
4. 计算$ a^2b^2 - \left( \frac{a^2 + b^2 - c^2}{2} \right)^2$：
$24 - \frac{1}{4} = \frac{96}{4} - \frac{1}{4} = \frac{95}{4}$
5. 计算$ \frac{1}{4} × \left[ a^2b^2 - \left( \frac{a^2 + b^2 - c^2}{2} \right)^2 \right]$：
$\frac{1}{4} × \frac{95}{4} = \frac{95}{16}$
6. 最后，计算 S：
$S = \sqrt{\frac{95}{16}} = \frac{\sqrt{95}}{4}$
【答案】：
$\frac{\sqrt{95}}{4}$

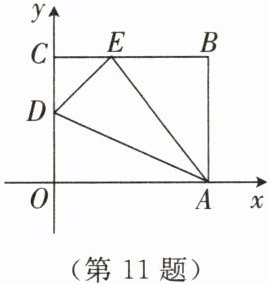
11. 如图，$OABC$是一张放在平面直角坐标系中的长方形纸片，$O$为原点，点$A$在$x$轴的正半轴上，点$C$在$y$轴的正半轴上，$OA = 10$，$OC = 8$。在$OC$边上取一点$D$，将纸片沿$AD$翻折，使点$O$落在$BC$边上的点$E$处，则点$D$的坐标是(0,5)。

答案： （0，5）
解：
∵四边形OABC是长方形，OA=10，OC=8，
∴BC=OA=10，AB=OC=8，点A（10，0），点B（10，8），点C（0，8）。
由翻折性质得：AE=AO=10，DE=DO。
设D（0，d），则OD=d，DC=8-d，DE=d。
在Rt△ABE中，$BE=\sqrt{AE^{2}-AB^{2}}=\sqrt{10^{2}-8^{2}}=6，$
∴CE=BC-BE=10-6=4，即点E（4，8）。
在Rt△DCE中，DC²+CE²=DE²，即（8-d）²+4²=d²，
解得d=5，
∴点D的坐标是（0，5）。
答案：（0，5）

12. 在$\triangle ABC$中，$AB = AC = 5cm$。若$\triangle ABC$一边上的高为$4cm$，则$BC$的长为2$\sqrt{5}$cm或4$\sqrt{5}$cm或6cm。

答案： $​ 6\ \mathrm {cm} {或2}\sqrt 5\ \mathrm {cm} {或4}\sqrt 5\ \mathrm {cm}​$
解：情况一：高在底边BC上
∵AB=AC=5cm，高AD=4cm
∴BD=DC
在Rt△ABD中，BD²=AB²-AD²=5²-4²=9
∴BD=3cm
∴BC=2BD=6cm
情况二：高在腰AB上
过C作CE⊥AB于E，CE=4cm
在Rt△ACE中，AE²=AC²-CE²=5²-4²=9
∴AE=3cm
∴BE=AB-AE=5-3=2cm
在Rt△BCE中，BC²=BE²+CE²=2²+4²=20
∴BC=2√5cm
情况三：高在腰AC上，同理可得BC=2√5cm
综上，BC的长为6cm或2√5cm。

13. 计算。
(1) $(-1)^2-\sqrt[3]{27}+\sqrt{4}$；
(2) $(\pi - 2025)^0-|\sqrt{3}-2|-\sqrt{12}$。

答案： =1-3+2
=0
$​=1-(2-\sqrt 3)-2\sqrt 3​$
$​= -1 - \sqrt {3}​$

14. 已知$2a + 1$的算术平方根是$3$，$3a - b - 1$的立方根是$2$。
(1) 求$a$，$b$的值。
(2) 求$20b + a$的平方根。

答案： 解：​
(1)​
∵​2a+1​的算术平方根是​3​
∴​2a+1=9​
解得​a=4​
∵​3a-b-1​的立方根是​2​
∴​3a-b-1=8​
∴​3×4-b-1=8​
解得​b=3​
​
(2)​由​
(1)​可知​a=4，​​b=3​
∴​20b+a=20×3+4=64​
∵​64​的平方根是​±8​
∴​20b+a​的平方根是​±8​

15. 如图，已知$AB = CD = 6dm$，$BC = 3dm$，$AD = 9dm$，$\angle ABD = 90^{\circ}$。请说明：$BC\perp CD$。

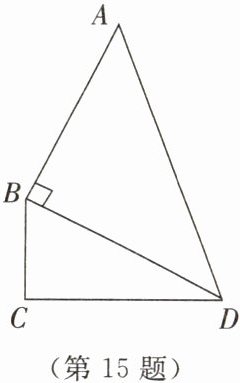
答案： 解：在​ Rt △ABD ​中
$​BD^2=AD^2-AB^2=9^2-6^2=45​$
在​△ BCD ​中，$​BC^2+CD^2=3^2+6^2=45​$
∴$​BC^2+CD^2=BD^2​$
∴​∠BCD=90°，​
∴​BC⊥CD​
【解析】：本题主要考查勾股定理和其逆定理的应用。
先利用勾股定理求出BD的长度，再利用勾股定理的逆定理判断三角形BCD是否为直角三角形，从而得出BC与CD是否垂直。