《2025年作业本江西教育出版社八年级数学上册北师大版》

1. 学校举行演讲比赛，7 位评委给选手甲的评分如下：95，93，89，91，88，94，95。这组数据的中位数和众数分别是(C)

A.91，95
B.95，91
C.93，95
D.95，93

答案： C
【解析】：
本题主要考查中位数和众数的概念及求解方法。
中位数：把一组数据从小到大排序后，位于中间位置的数值。如果数据量是奇数，则中位数是中间那个数；如果数据量是偶数，则中位数是中间两个数的平均值。
众数：一组数据中出现次数最多的数。
首先，我们把评委的评分从小到大排序：
88, 89, 91, 93, 94, 95, 95，
因为数据量是奇数（7个数据），所以中位数就是排序后位于中间的数，即第4个数：93。
接下来，我们观察哪个数出现的次数最多。从排序后的数据中可以看出，95出现了2次，而其他数都只出现了1次。因此，众数是95。
综上所述，这组数据的中位数是93，众数是95。
【答案】：C

2. 甲、乙、丙、丁四名运动员各进行 20 次射击测试，他们的平均成绩相同，方差分别是 $ s_{甲}^{2}=2.1 $，$ s_{乙}^{2}=1.1 $，$ s_{丙}^{2}=1.5 $，$ s_{丁}^{2}=0.9 $。这四名运动员成绩最稳定的是(D)

A.甲
B.乙
C.丙
D.丁

答案： D
解：
∵方差是衡量数据波动大小的量，方差越小，数据越稳定。
又
∵$s^{2}_{甲}= 2.1，$$s^{2}_{乙}= 1.1，$$s^{2}_{丙}= 1.5，$$s^{2}_{丁}= 0.9，$
且0.9 ＜ 1.1 ＜ 1.5 ＜ 2.1，即$s^{2}_{丁} ＜ s^{2}_{乙} ＜ s^{2}_{丙} ＜ s^{2}_{甲}，$
∴成绩最稳定的是丁。
答案：D

3. 若 $ x_{1} $，$ x_{2} $，$·s$，$ x_{10} $ 的平均数是 10，$ x_{11} $，$ x_{12} $，$·s$，$ x_{30} $ 的平均数是 20，则 $ x_{1} $，$ x_{2} $，$·s$，$ x_{30} $ 的平均数是(D)

A.10
B.20
C.15
D.$ \frac{50}{3} $

答案： D
解：
∵$ x_{1},x_{2},…,x_{10} $的平均数是10，
∴$ x_{1}+x_{2}+…+x_{10}=10×10=100。$
∵$ x_{11},x_{12},…,x_{30} $的平均数是20，
∴$ x_{11}+x_{12}+…+x_{30}=20×20=400。$
∴$ x_{1}+x_{2}+…+x_{30}=100+400=500。$
∴ 这30个数的平均数为$ \frac{500}{30}=\frac{50}{3}。$
答案：D

4. 体育组为了了解八年级学生 1 min 跳绳次数的情况，随机抽取了 20 名八年级学生进行 1 min 跳绳测试(单位：次)，数据如下：
100，110，114，114，120，122，122，131，144，148，152，155，156，165，165，165，165，174，188，190。
学生跳绳次数的下四分位数是121次，上四分位数是165次。

答案： 121
165
解：将20个数据按从小到大排列：100,110,114,114,120,122,122,131,144,148,152,155,156,165,165,165,165,174,188,190。
下四分位数位置：20×25\% = 5，为第5项与第6项的平均数，即$\frac{120 + 122}{2} = 121。$
上四分位数位置：20×75\% = 15，为第15项与第16项的平均数，即$\frac{165 + 165}{2} = 165。$
121；165

5. 一组数据 2，$ x $，4，2，3，5 的平均数为 3，这组数据的方差为$\frac{4}{3}$。

答案： $\frac{4}{3}$
解：因为数据2,x,4,2,3,5的平均数为3，
所以$\frac{2 + x + 4 + 2 + 3 + 5}{6} = 3，$
解得x = 2。
这组数据为2,2,4,2,3,5。
方差$s^{2}=\frac{1}{6}[(2 - 3)^{2} + (2 - 3)^{2} + (4 - 3)^{2} + (2 - 3)^{2} + (3 - 3)^{2} + (5 - 3)^{2}]$
$=\frac{1}{6}[(-1)^{2} + (-1)^{2} + 1^{2} + (-1)^{2} + 0^{2} + 2^{2}]$
$=\frac{1}{6}(1 + 1 + 1 + 1 + 0 + 4)$
$=\frac{1}{6}×8$
$=\frac{4}{3}$
$\frac{4}{3}$

6. 甲、乙两名射击运动员在相同条件下各射击 6 次，甲的成绩(单位：环)为 8，8，9，10，5，8，乙的成绩(单位：环)为 6，10，6，10，9，7。这两名运动员中发挥得更稳定的是甲(填“甲”或“乙”)。

答案： 解：甲的平均成绩：$\overline{x}_{甲}=\frac{8+8+9+10+5+8}{6}=\frac{48}{6}=8（$环）
甲的方差：$s^{2}_{甲}=\frac{(8-8)^{2}+(8-8)^{2}+(9-8)^{2}+(10-8)^{2}+(5-8)^{2}+(8-8)^{2}}{6}=\frac{0+0+1+4+9+0}{6}=\frac{14}{6}\approx2.33$
乙的平均成绩：$\overline{x}_{乙}=\frac{6+10+6+10+9+7}{6}=\frac{48}{6}=8（$环）
乙的方差：$s^{2}_{乙}=\frac{(6-8)^{2}+(10-8)^{2}+(6-8)^{2}+(10-8)^{2}+(9-8)^{2}+(7-8)^{2}}{6}=\frac{4+4+4+4+1+1}{6}=\frac{18}{6}=3$
因为2.33＜3，即$s^{2}_{甲}＜s^{2}_{乙}，$所以甲发挥得更稳定。
甲

7. 下图是某市 2023 年、2024 年 8 月上旬日最高气温的折线统计图。

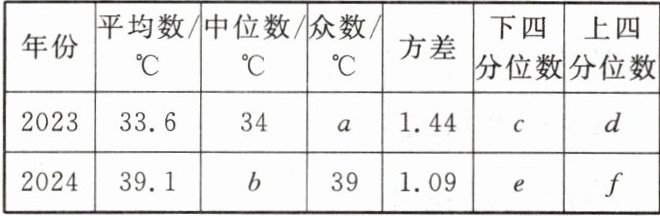
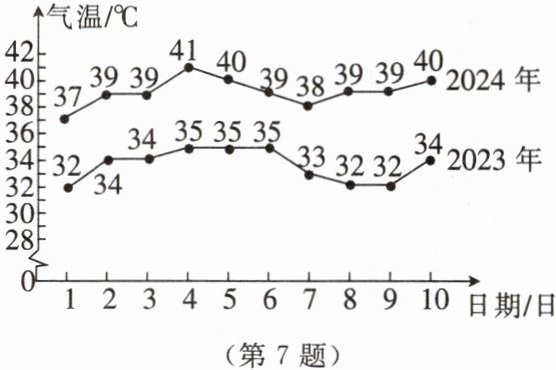
（1）根据统计图中的信息，求 $ a $，$ b $，$ c $，$ d $，$ e $，$ f $ 的值。
（2）请你从两个不同的角度比较该市 2023 年、2024 年 8 月上旬的日最高气温。

答案：
(1)解：2023年8月上旬日最高气温（℃）：32,34,34,35,35,35,33,32,32,34
排序：32,32,32,33,34,34,34,35,35,35
众数a=32,34,35（出现次数最多，均为3次）
下四分位数位置：(10+1)×0.25=2.75，c=32
上四分位数位置：(10+1)×0.75=8.25，d=35
2024年8月上旬日最高气温（℃）：37,39,39,41,40,39,38,39,39,40
排序：37,38,39,39,39,39,39,40,40,41
中位数b=(39+39)/2=39
下四分位数位置：(10+1)×0.25=2.75，e=39
上四分位数位置：(10+1)×0.75=8.25，f=40
(2)①从平均数看：2024年（39.1℃）高于2023年（33.6℃），2024年8月上旬整体气温更高；
②从方差看：2024年（1.09）小于2023年（1.44），2024年气温波动更小，更稳定。