《2025年作业本江西教育出版社八年级数学上册北师大版》

8. 如图，我们把杜甫的《绝句》整齐地排列在平面直角坐标系中。
(1)“岭”的坐标是(4,2)，“船”的坐标是(7,1)。
(2)将第$2$行“窗含西岭千秋雪”与第$3$行“一行白鹭上青天”对调，再将第$3$列与第$7$列对调，“雪”由开始的坐标依次变换为(7,3)和(3,3)。
(3)“泊”开始的坐标是$(2,1)$，若要使它的坐标变换到$(5,3)$，应该哪两行和哪两列对调？

答案： (4，2)
(7，1)
(7，3)
(3，3)
解：
(3)应该将第 1 行与第 3 行对调，
再将第 2 列与第 5 列对调。

9. 如图，在平面直角坐标系中，$\triangle ABC$的顶点都在格点上。
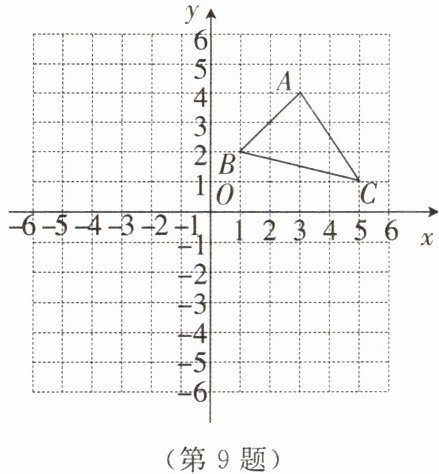
（1）若$\triangle ABC$各顶点的横坐标不变，纵坐标都乘$-1$，请你在同一平面直角坐标系中描出对应的点$A'$，$B'$，$C'$，并依次连接这三个点得到$\triangle A'B'C'$。观察并说明$\triangle A'B'C'$与$\triangle ABC$的位置关系。
（2）求$\triangle ABC$的面积。
（3）已知$P$为$x$轴上一点，若$\triangle BB'P$的面积是$\triangle ABC$面积的$3$倍，求此时点$P$的坐标。

答案：

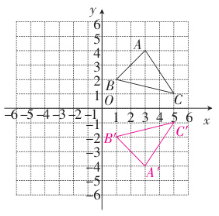
解：​
(1)​如图，​ △A'B'C'​与​△ABC​关于​x​轴对称
$​(2)S_{△ABC}=4×3-\frac 12×2×3-\frac 12×2×2​$
$​-\frac 12×1×4=5​$
​
(3)​设​ BB'P ​的边​BB'​上的高为​h，​
点​P ​的坐标为​(x，​​0)​
∵​BB'=4，​且​△BB'P ​的面积是​△ABC​面积的​3​倍
∴$​\frac 12×4\ \mathrm {h}=3×5，$​解得$​h=\frac {15}2​$
当点​P ​在​x​轴负半轴时，
$​x=1-\frac {15}2=-\frac {13}2​$
当点​P ​在​x​轴正半轴时，
$​x=1+\frac {15}2=\frac {17}2​$
∴点​P ​的坐标为$​(-\frac {13}2，$​​0)​或$​(\frac {17}2，$​​0)​