第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
7. 科学研究发现,空气中的含氧量$y$(单位:$\%$)与海拔$x$(单位:$m$)之间近似地满足一次函数关系。经测量,海拔为$0\ m$时,空气中的含氧量为$21\%$。已知某山山脚某处海拔为$2400\ m$,测得空气中的含氧量约为$17\%$。
(1)求空气中的含氧量$y$与海拔$x$之间的关系式。
(2)当空气中的含氧量低于$14\%$时,登山运动员需要佩戴氧气瓶补充氧气。已知该山能到达的最高点海拔为$4680\ m$,试判断登山运动员是否需要提前准备氧气瓶,并说明理由。
(1)求空气中的含氧量$y$与海拔$x$之间的关系式。
(2)当空气中的含氧量低于$14\%$时,登山运动员需要佩戴氧气瓶补充氧气。已知该山能到达的最高点海拔为$4680\ m$,试判断登山运动员是否需要提前准备氧气瓶,并说明理由。
答案:
解:
(1)设y=kx+b(k≠0)
依题意得$\begin {cases}{2400k+b=17}\\{b=21}\end {cases},$解得$\begin {cases}{k=-\frac 1{600}}\\{b=21}\end {cases}$
∴y与x之间的关系式为$y=-\frac 1{600}x+21$
(2)需要,理由如下:
当空气中的含氧量为14\%时,
$-\frac 1{600}x+21=14$
解得x=4200
∵4200<4680
∴登山运动员需要提前准备氧气瓶
(1)设y=kx+b(k≠0)
依题意得$\begin {cases}{2400k+b=17}\\{b=21}\end {cases},$解得$\begin {cases}{k=-\frac 1{600}}\\{b=21}\end {cases}$
∴y与x之间的关系式为$y=-\frac 1{600}x+21$
(2)需要,理由如下:
当空气中的含氧量为14\%时,
$-\frac 1{600}x+21=14$
解得x=4200
∵4200<4680
∴登山运动员需要提前准备氧气瓶
8. 如图,直线$y = kx + b$($k\neq 0$)与坐标轴分别交于$A$,$B$两点,$OA = 8$,$OB = 6$,点$M(3,m)$在直线上。动点$P$从点$A$出发,以每秒$1$个单位长度的速度沿路线$A\to O\to B$运动,到达点$B$时运动停止。设点$P$的运动时间为$t\ s$。
(1)求点$M$的坐标。
(2)用含$t$的代数式表示$OP$的长度。
(3)当$t = 3$时,求$\triangle OPM$的面积。
(4)当$\triangle OPM$的面积为$6$时,求$t$的值。
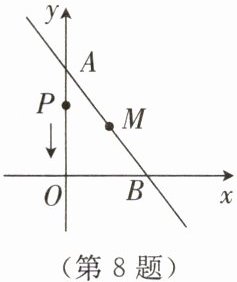
(1)求点$M$的坐标。
(2)用含$t$的代数式表示$OP$的长度。
(3)当$t = 3$时,求$\triangle OPM$的面积。
(4)当$\triangle OPM$的面积为$6$时,求$t$的值。

答案:
∴直线$ AB $的表达式为$y=-\frac 43x+8$
解:$(1)$依题意,得点$ A $的坐标为$(0,$$8),$
点$ B $的坐标为$(6,$$0)$
设直线$ AB $的表达式为$y=kx+8$
将$B(6,$$0)$代入,得$k=-\frac 43$
∴直线$ AB $的表达式为$y=-\frac 43x+8$
当$x=3$时,$y=4,$所以点$ M $的坐标为$(3,$$4)$
$(2)$当点$ P $在$ OA $上,即$0≤t≤8$时,$AP=t$
所以$OP=8-t$
当点$ P $在$OB $上,即$8<t≤14$时
$OP=t-8$
综上所述,$OP=\begin {cases}{8-t(0≤t≤8)}\\{t -8(8<t≤14)}\end {cases}$
$(3)S_{△OPM}=\frac 12OP·|x_{M}|$
$=\frac 12×5×3=\frac {15}2$
$(4)$当$0≤t≤8$时,根据题意,
得$S_{△OPM}=\frac 12OP·|x_{M}|$
$=\frac 12×(8-t)×3=6,$解得$t=4$
当$8<t≤14$时,根据题意,
得$S_{△OPM}=\frac 12OP·|y_{M}|$
$=\frac 12×(t-8)×4=6,$解得$t=11$
综上所述,当$△OPM$的面积为$ 6 $时,
$t $的值为$ 4 $或$ 11$
查看更多完整答案,请扫码查看


