《2025年作业本江西教育出版社八年级数学上册北师大版》

1. 一个两位数的十位数字与个位数字之和是 8。若将这个两位数加上 18，所得结果恰好是把这个两位数的个位数字和十位数字对调后组成的数，则这个两位数是35。

答案： 35
解：设这个两位数的十位数字为x，个位数字为y。
依题意，得$\begin{cases}x + y = 8 \\10x + y + 18 = 10y + x\end{cases}$
由第二个方程化简得：9x - 9y = -18，即x - y = -2
联立$\begin{cases}x + y = 8 \\x - y = -2\end{cases}$
两式相加得：2x = 6，解得x = 3
将x = 3代入x + y = 8，得y = 5
所以这个两位数是10x + y = 10×3 + 5 = 35
答：这个两位数是35。

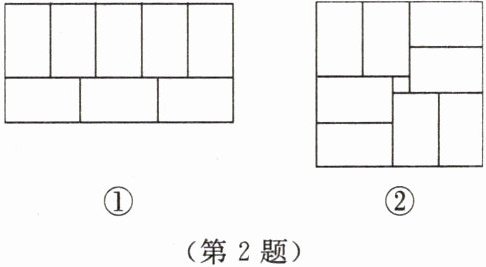
2. 8 个大小一样的小长方形恰好可以拼成一个大长方形，如图①所示。若拼成如图②所示的正方形，则中间还留下一个边长为 2 cm 的小正方形。一个小长方形的长为10cm，宽为6cm。

答案： 10
6
解：设小长方形的长为xcm，宽为ycm。
由图①得：5y = 3x
由图②得：2y - x = 2
解得：x = 10，y = 6
10，6

3. 甲、乙两船相距 42 n mile，相向而行，2 h 后相遇；同向而行，甲 14 h 后追上乙。水流速度忽略不计，甲船的速度为12n mile/h，乙船的速度为9n mile/h。

答案： 12
9
解：设甲船的速度为x n mile/h，乙船的速度为y n mile/h。
根据相向而行，2 h后相遇，可列方程：2(x + y) = 42
根据同向而行，甲14 h后追上乙，可列方程：14(x - y) = 42
化简方程组得：
$\begin{cases}x + y = 21 \\ x - y = 3\end{cases}$
将两式相加：2x = 24，解得x = 12
将x = 12代入x + y = 21，得12 + y = 21，解得y = 9
甲船的速度为12 n mile/h，乙船的速度为9 n mile/h。

4. 一座桥长 2000 m，一列火车匀速行驶，从车头上桥到车尾离桥用了 1 min，完全在桥上的时间为 40 s。火车的长度为400m，行驶速度为40m/s。

答案： 400
40
【解析】：
本题主要考查二元一次方程组的应用。
设火车的长度为x米，行驶速度为y m/s。
当火车从车头上桥到车尾离桥时，火车行驶的距离是桥长加上火车的长度，即2000 + x米。
根据题意，这段时间是1分钟，即60秒，所以有方程：
60y = 2000 + x，
当火车完全在桥上时，火车行驶的距离是桥长减去火车的长度，即2000 - x米。
根据题意，这段时间是40秒，所以有方程：
40y = 2000 - x，
将两个方程组合，得到二元一次方程组：
$\begin{cases}60y = 2000 + x \\40y = 2000 - x\end{cases}$
解这个方程组，得到：
$\begin{cases}x = 400 \\y = 40\end{cases}$
所以，火车的长度是400米，行驶速度是40 m/s。
【答案】：
火车的长度为400m，行驶速度为40m/s。

5. 小明从家到学校需要先走一段上坡路再走一段下坡路。如果小明上坡平均每小时走 2 km，下坡平均每小时走 3 km，那么从家走到学校需要 15 min；如果放学回家时，小明上坡和下坡的平均速度不变，那么从学校回家需要 20 min。小明家与学校的距离是多少千米？

答案： 解：设小明从家到学校的上坡路程为$​x\mathrm {km}，$​
下坡路程为$​y\mathrm {km}​$
据题意得$​\begin {cases}{\frac {x}2+\frac {y}3=\frac {15}{60}}\\{\frac y 2+\frac {x}3=\frac {20}{60}}\end {cases}​$
解得$​\begin {cases}{x=0.1}\\{y=0.6}\end {cases}​$
∴​x+y=0.7​
答：小明家与学校的距离是$​0.7\ \mathrm {km}。$​

6. 甲、乙两人在 400 m 的环形路上匀速跑步。如果同时同地出发，反向而行，每隔 2 min 相遇一次；如果同时同地出发，同向而行，每隔 6 min 相遇一次。已知甲比乙跑得快。
（1）求甲、乙两人的速度。
（2）甲、乙两人跑一圈各需要多少分钟？

答案： 解：​
(1)​设甲的速度为$​x\ \mathrm {m/}\mathrm {\mathrm {min}}，$​
乙的速度为$​y\ \mathrm {m/}\mathrm {\mathrm {min}}​$
依题意得$​\begin {cases}{2(x+y)=400}\\{6(x-y)=400}\end {cases}​$
解得$​\begin {cases}{x=\frac {400}3}\\{y=\frac {200}3}\end {cases}​$
答：甲的速度为$​\frac {400}3\ \mathrm {m/}\mathrm {\mathrm {min}}，$​
乙的速度为$​\frac {200}3\ \mathrm {m/}\mathrm {\mathrm {min}}​$
​
(2)​甲跑一圈需要$​400÷\frac {400}3=3 (\mathrm {\mathrm {min}})，$​
乙跑一圈需要$​400÷\frac {200}3=6 (\mathrm {\mathrm {min}})​$
答：甲跑一圈需要$​3 \mathrm {\mathrm {min}}，$​乙跑一圈需要$​6 \mathrm {\mathrm {min}}。$​