《2025年作业本江西教育出版社八年级数学上册北师大版》

1. 学校食堂有15元、18元、20元三种价格的盒饭供学生选择(每人购一份)。某天的盒饭销售情况如图所示，则当天学生购买盒饭费用的平均数是(C)

A.15元
B.16元
C.17元
D.18元
]

答案： C
【解析】：本题考查的是平均数的计算。
由图可知，15元盒饭占比40\%，18元盒饭占比50\%，20元盒饭占比10\%。
根据加权平均数公式：$\bar{x}=\frac{x_{1}f_{1}+x_{2}f_{2}+\cdots+x_{n}f_{n}}{f_{1}+f_{2}+\cdots+f_{n}}（$其中$x_{i}$为各数据，$f_{i}$为各数据的权数）。
这里$x_{1}=15，$$f_{1}=40\%；$$x_{2}=18，$$f_{2}=50\%；$$x_{3}=20，$$f_{3}=10\%。$
则平均数$\bar{x}=15×40\% + 18×50\% + 20×10\%$
=15×0.4 + 18×0.5 + 20×0.1
=6 + 9 + 2
= 17（元）
【答案】：C

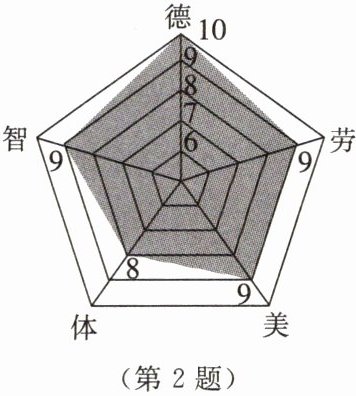
2. 某校学生期末操行评定从德、智、体、美、劳五个方面进行考核，五个方面的得分按3：2：2：2：1的比例确定最终成绩。小明本学期五个方面的得分如图所示，他的期末操行最终成绩为(B)

A.9
B.9.1
C.45
D.91
]

答案： B
解：由图可知，小明德、智、体、美、劳五个方面的得分分别为10、9、8、9、9。
五个方面的得分比例为3:2:2:2:1，总份数为3+2+2+2+1=10。
最终成绩 = (10×3 + 9×2 + 8×2 + 9×2 + 9×1)÷10
= (30 + 18 + 16 + 18 + 9)÷10
= 91÷10
= 9.1
答案：B

3. 在一次体育课上，体育老师对八年级(1)班的50名同学进行了立定跳远项目的测试，测试所得分数及相应的人数如图所示。这50名学生的平均得分为8.9分。

答案： 8.9
【解析】：
本题考查平均数的计算。
平均数的计算公式为：所有数据的总和除以数据的个数。
在本题中，需要将每个分数段的人数乘以该分数，然后将得到的结果相加，再除以总人数，即可得到平均得分。
具体计算过程如下：
计算每个分数段的总得分：
7分段：7× 5 = 35(分)，
8分段：8 × 10 = 80(分)，
9分段：9× 20 = 180(分)，
10分段：10× 15 = 150(分)，
计算所有学生的总得分：
35 + 80 + 180 + 150 = 445(分)，
计算平均得分：
总得分除以总人数，即445 ÷ 50 = 8.9(分)。
【答案】：
8.9。

4. 若$x_{1}$，$x_{2}$，…，$x_{10}$的平均数是a，$x_{11}$，$x_{12}$，…，$x_{30}$的平均数是b，则$x_{1}$，$x_{2}$，…，$x_{30}$的平均数是$\frac{a + 2b}{3}$。

答案： $\frac{a + 2b}{3}$
【解析】：
这个问题考查的是平均数的计算。
首先，我们已知两组数的平均数，要求合并后的大组的平均数。
平均数的定义是所有数的和除以数的个数。
第一组数$x_1,x_2,…,x_{10}$的平均数是a，所以这10个数的和是10a。
第二组数$x_{11},x_{12},…,x_{30}$的平均数是b，所以这20个数的和是20b。
两组数合并后，总数是30个数，其和是10a + 20b。
所以，$x_1,x_2,…,x_{30}$的平均数是$\frac{10a + 20b}{30}，$简化后得到$\frac{a + 2b}{3}。$
【答案】：
$\frac{a + 2b}{3}。$

5. 某单位招聘员工，采取笔试和面试相结合的方式进行，6名应聘者的成绩（满分均为100分）如下表所示：

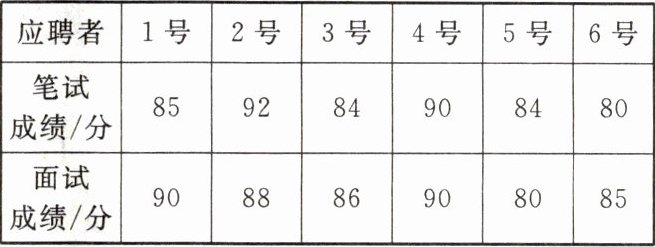
根据规定，笔试成绩和面试成绩分别按一定的百分比折合成综合成绩（综合成绩满分仍为100分）。
（1）已知1号应聘者的综合成绩为88分，分别求出笔试成绩和面试成绩在综合成绩中所占的百分比。
（2）在（1）的条件下，求2号应聘者的综合成绩。

答案： 解：$​$　　
$(1)​$设笔试成绩和面试成绩所占的　　
百分比分别是$​x，$$​​y​$　　
根据题意得$​\begin {cases}{x+y=1}\\{85x+90y=88}\end {cases}​$　　
解得$​\begin {cases}{x=0.4=40\%}\\{y=0.6=60\% }\end {cases}​$　　
答：笔试成绩和面试成绩所占的百分比　　
分别是$​40\%，$$​​60\%。$$​$　　
$​$　　
$(2)92×40\%+88×60\%=89.6(​$分$​)​$　　
答：$​2​$号应聘者的综合成绩是$​89.6​$分。