《2025年作业本江西教育出版社八年级数学上册北师大版》

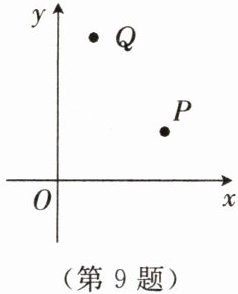
9. 如图，在平面直角坐标系中有$P$，$Q$两点，其坐标分别为$(5,a)$，$(b,7)$。
(1)比较大小：$a$＜$7$，$b$＜$5$。(填“$＞$”“$＜$”或“$=$”)
(2)判断点$(6 - b,a - 10)$在第几象限，并说明理由。

答案： ＜
＜
解：​
(2)​点​(6-b，​​a-10)​在第四象限
理由如下：
∵​a＜7，​​b＜5​
∴​6-b＞0，​​a-10＜0​
∴点​(6-b，​​a-10)​在第四象限

10. 已知平面直角坐标系中有一点$M(2m + 1,m + 3)$。
（1）若点$M$在第一象限，且点$M$到$x$轴的距离是到$y$轴距离的$2$倍，求$m$的值。
（2）若点$N$的坐标为$(2,1)$，且$MN// x$轴，求点$M$的坐标。

答案： 解：​
(1)​
∵点​M​在第一象限，且点​M​到​x​轴
的距离是到​y​轴距离的​2​倍
∴​2(2m+1)=m+3，​
∴$​m=\frac 13​$
​
(2)​
∵​MN//x​轴
∴​M，​​N​两点的纵坐标相等
∴​m+3=1，​
∴​m=-2​
∴点​M​的坐标为​(-3，​​1)​
【解析】：
本题主要考察平面直角坐标系中点的坐标与象限的关系，以及平行于坐标轴的线段上点的坐标特点。
(1) 对于点M在第一象限，其横纵坐标都应为正数。根据题意，点M到x轴的距离是纵坐标的绝对值，即|m+3|，到y轴的距离是横坐标的绝对值，即|2m+1|。由于点M在第一象限，所以m+3和2m+1都为正，可以去掉绝对值符号。根据题意，有m+3=2(2m+1)，解这个方程得到m的值。
(2) 对于线段MN平行于x轴，意味着点M和点N的纵坐标相等。根据题意，有m+3=1，解这个方程得到m的值，再代入2m+1求得点M的横坐标。

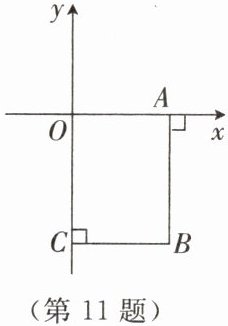
11. 如图，在平面直角坐标系中，$AB\perp x$轴，垂足为$A$，$BC\perp y$轴，垂足为$C$。已知$A(a,0)$，$C(0,c)$，其中$a$，$c$满足$(a - 6)^2+\sqrt{c + 8}=0$。点$P$从点$O$出发，沿$O\to A\to B\to C$的方向运动到点$C$停止，运动速度为每秒$2$个单位长度，设点$P$的运动时间为$t\ s$。
（1）在运动过程中，当点$P$到$AB$的距离为$2$个单位长度时，求点$P$运动的时间。
（2）在点$P$的运动过程中，用含$t$的代数式表示点$P$的坐标。

答案： 解：​
(1)​
∵$​(a-6)^2+\sqrt {c+8}=0​$
∴​a-6=0，​​c+8=0​
∴​a=6，​​c=-8​
∴​A(6，​​0)，​​C(0，​​-8)​
∴​AO=BC=6，​​AB=OC=8​
​①​点​P ​在​AO​上，当点​P ​到​AB​的距离为​2​个
单位长度时，​AP=2​
∴​OP=6-2=4，​
∴$​2\ \mathrm {t}=4，$​
∴​t=2​
​②​点​P ​在​BC​上，当点​P ​到​AB​的距离为​2​个
单位长度时，​BP=2​
∴​AO+AB+BP=6+8+2=16​
∴$​2\ \mathrm {t}=16，$​
∴​t=8​
综上所述，当点​P ​到​AB​的距离为​2​个
单位长度时，点​P ​运动的时间为$​2\ \mathrm {s} ​$或$​8\ \mathrm {s}​$
​
(2)①​当​0≤t≤3​时，$​P(2\ \mathrm {t}，$​​0)​
​②​当​3＜t≤7​时，​P(6，$​​6-2\ \mathrm {t})​$
​③​当​7＜t≤10​时，$​P(20-2\ \mathrm {t}，$​​-8)​