《2025年作业本江西教育出版社八年级数学上册北师大版》

1. 某餐馆有 $ M $，$ N $，$ P $，$ Q $，$ R $，$ S $ 等特色菜，由于人手和食材限制，顾客需根据下列规则点菜：
①不能同时点 $ M $ 和 $ N $；
②如果点了 $ P $，就要点 $ Q $ 或 $ R $；
③在 $ Q $ 和 $ S $ 中必须点一个，且只能点一个。
下列组合符合点菜规则的是(C)

A.$ Q $，$ M $，$ N $
B.$ S $，$ N $，$ P $
C.$ P $，$ N $，$ Q $
D.$ M $，$ P $，$ R $

答案： C
解：
A. 由规则①，M和N不能同时点，A选项含M、N，不符合；
B. 由规则②，点P需点Q或R，B选项含P但不含Q、R，不符合；
C. 规则①：不含M和N同时出现，符合；规则②：含P且含Q，符合；规则③：含Q不含S，符合；
D. 由规则③，Q和S必须且只能点一个，D选项不含Q和S，不符合。
结论：C

2. 如图，一个 $ 4×4 $ 的正方形网格被分成了四块“”。若要求每块、每行、每列四个空格中均有“强”“国”“有”“我”四个汉字，则在★处应填入的汉字是(B)

A.强
B.国
C.有
D.我

答案： B

3. 有一本书，若每天读 $ 80 $ 页，则 $ 4 $ 天读不完，$ 5 $ 天又有余；若每天读 $ 90 $ 页，则 $ 3 $ 天读不完，$ 4 $ 天又有余；若每天读 $ n $($ n $ 是自然数)页，则恰好 $ n $ 天读完。这本书有 324 页。

答案： 324
解：设这本书有x页。
由每天读80页，4天读不完，5天有余，得80×4 ＜ x ＜ 80×5，即320 ＜ x ＜ 400。
由每天读90页，3天读不完，4天有余，得90×3 ＜ x ＜ 90×4，即270 ＜ x ＜ 360。
综合得320 ＜ x ＜ 360。
因每天读n页，恰好n天读完，所以$x = n^2（n$为自然数）。
在$320 ＜ n^2 ＜ 360$中，n = 18时，$n^2 = 324；$n = 19时，$n^2 = 361（$舍去）。
故x = 324。
答案：324

4. 若一个自然数被 $ 2 $ 除余 $ 1 $，被 $ 3 $ 除余 $ 2 $，被 $ 5 $ 除余 $ 3 $，则称这个数是“魅力数”。
（1）判断 $ 43 $ 是否为“魅力数”，请说明理由。
（2）求出所有不大于 $ 100 $ 的“魅力数”。

答案： 解：
(1)43 不是''魅力数''。理由如下：
∵43=14×3+1
∴ 43 被 3 除余 1，不余 2
∴ 43 不是''魅力数''
(2)先确定被 2 除余 1 且被 5 除余 3 的数，
有 13，23，33，43，53，63，73，83，93
再确定被 3 除余 2 的数，有 23，53，83
故所有不大于 100 的''魅力数''有 23，53，83

5. 如图，已知线段 $ a $ 和 $ \angle\alpha $，求作 $ \triangle ABC $，使 $ AB = a $，$ AC = 2a $，$ \angle A=\frac{1}{2}\angle\alpha $。（尺规作图，不写作法，保留作图痕迹）

答案：

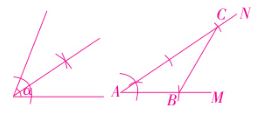
解：如图所示，$​\triangle ABC​$即为
所求作的三角形