《2025年作业本江西教育出版社八年级数学上册北师大版》

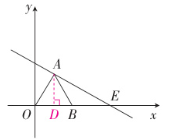
9. 如图，$ \triangle OAB $ 是边长为 $ 2 $ 的等边三角形，过点 $ A $ 的直线 $ y = -\dfrac{\sqrt{3}}{3}x + m $ 与 $ x $ 轴交于点 $ E $。
（1）求点 $ E $ 的坐标。
（2）请说明：$ OA \perp AE $。

答案：

解：​
(1)​过点​A​作​AD⊥EO​于点​D​
∵​∆OAB​是边长为​2​的等边三角形
∴​OD=DB=1，​​AB=AO=OB=2​
∴$​AD=\sqrt 3，$​
∴点​A​的坐标为​(1，$​​\sqrt 3)​$
将点​A​的坐标代入直线$​y=-\frac {\sqrt 3}3x+m​$
得$​\sqrt 3=-\frac {\sqrt 3}3+m，$​解得$​m=\frac {4\sqrt 3}3​$
∴$​y=-\frac {\sqrt 3}3x+\frac {4\sqrt 3}3​$
当​y=0​时，​x=4，​即点​E​的坐标为​(4，​​0)​
​
(2)​
∵$​AD=\sqrt 3，$​​DE=EO - DO=3​
∴$​AE=\sqrt {3^2+(\sqrt 3)^2}=2\sqrt 3​$
∵$​AO^2 + AE^2 = 16，$$​​EO^2 = 16​$
∴$​AO^2 + AE^2 = EO^2​$
∴​OA⊥AE​

10. 如图，已知直线 $ y_1 = x + 3 $ 与坐标轴交于 $ A $，$ B $ 两点，直线 $ y_2 = -\dfrac{1}{2}x - 3 $ 与坐标轴交于 $ C $，$ D $ 两点，两直线的交点为 $ M $。
（1）求点 $ M $ 的坐标。
（2）若在 $ x $ 轴上存在一点 $ T $，使得 $ S_{\triangle ATM} = S_{\triangle ADM} $，求出此时点 $ T $ 的坐标。

答案： 解：​
(1)​联立直线$​ y_{1}=x+3 ​$和直线$​y_{2}=-\frac 12x-3​$
可得$​ x+3=-\frac 12x-3​$
解得​ x=-4​
将​ x=-4 ​代入$​ y_{1}=x+3，$​得​ y=-1​
∴点​ M ​的坐标为​ (-4，​​-1)​
​
(2)​
∵$​y_{1}=x+3，$$​​y_{2}=-\frac 12x-3​$
当​ x=0 ​时，$​y_{1}=3，$$​​y_{2}=-3；$​
当$​ y_{1}=0 ​$时，​x=-3​
∴​A(0，​​3)，​​B(-3，​​0)，​​D(0，​​-3)​
∴​AD=6​
设点​ T(m，​​0)，​
∴​BT= |m+3 |​
∵$​S_{ △ADM}=\frac 12\ \mathrm {A}D·$|$x_{M}$|$ =\frac 12×6×4=12​$
∴$​S_{ △ATM}=S_{ △ATB}+S_{△ BTM}​$
$​=\frac 12× $|m+3| ×4=2|m +3| =12​
∴​|m+3| =6，​
∴​m=-9 ​或​ m=3​
∴点​ T ​的坐标为​ (-9，​​0) ​或​ (3，​​0)​