《2025年作业本江西教育出版社八年级数学上册北师大版》

1. 杆秤是一种利用杠杆原理来称量物品质量的简易装置，其秤砣到秤毫的水平距离$y$(单位：$cm$)与所挂物体的质量$x$(单位：$kg$)之间满足一次函数关系，如下表所示。$y$与$x$之间的关系式为$y = 5.5x + 2.5$。

答案： y = 5.5x + 2.5
【解析】：本题可先设出一次函数的表达式，再将表格中的两组数据代入表达式，得到关于未知系数的方程组，最后解方程组求出系数，进而得到函数关系式。
设y与x之间的关系式为y = kx + b（k，b为常数，$k\neq0）。$
把x = 1，y = 8.0和x = 2，y = 13.5分别代入y = kx + b中，得到方程组$\begin{cases}k + b = 8.0\\2k + b = 13.5\end{cases}。$
用第二个方程2k + b = 13.5减去第一个方程k + b = 8.0，消去b可得：
(2k + b)-(k + b)=13.5 - 8.0
2k + b - k - b = 5.5
k = 5.5
把k = 5.5代入k + b = 8.0，可得：
5.5 + b = 8.0
b = 8.0 - 5.5 = 2.5
所以y与x之间的关系式为y = 5.5x + 2.5。
将x = 3，y = 19.0代入y = 5.5x + 2.5进行验证：
当x = 3时，y = 5.5×3 + 2.5 = 16.5 + 2.5 = 19.0，与表格中数据一致，说明所求关系式正确。
【答案】：y = 5.5x + 2.5

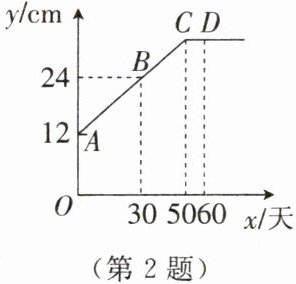
2. 某数学兴趣小组观察记录了莴笋的成长过程，绘制了莴笋的高度$y$(单位：$cm$)与观察时间$x$(单位：天)之间的函数图象，如图所示($CD$平行于$x$轴)。由图象可知，莴笋在第$60$天时的高度是32$cm$。
]

答案： 32
解：设线段AC的函数表达式为y = kx + b。
由图可知，点A(0,12)，点B(30,24)在AC上，将其代入表达式得：
$\begin{cases}b = 12 \\30k + b = 24\end{cases}$
解得k = 0.4，b = 12，所以y = 0.4x + 12。
当x = 50时，y = 0.4×50 + 12 = 32。
因为CD平行于x轴，所以当$x \geq 50$时，y = 32。
当x = 60时，y = 32。
32

3. 某地出租车的计费方式如图所示，$x$(单位：$km$)表示行驶里程，$y$(单位：元)表示车费。
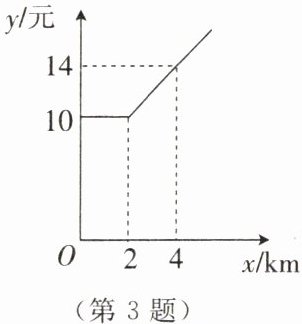
(1)该地出租车的起步价是10元。
(2)当$x＞2$时，超过$2km$的部分，每千米收费2元，$y$与$x$之间的关系式是$y = 2x + 6$。
(3)若某乘客乘坐出租车的里程为$18km$，则该乘客需支付车费42元。

答案：
(1)10
(2)2；y=2x+6
(3)42

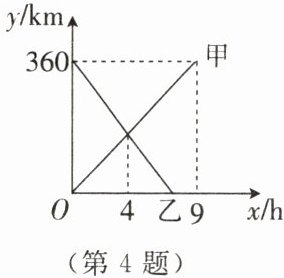
4. $A$，$B$两地相距$360km$，甲、乙两人分别从$A$，$B$两地同时出发，相向而行。甲、乙两人离$A$地的距离$y$（单位：$km$）与行驶时间$x$（单位：$h$）之间的函数图象如图所示。
（1）分别求出$y_{甲}$，$y_{乙}$与$x$之间的关系式。
（2）求当乙到达$A$地时，甲与$B$地的距离。
（3）如果甲、乙两人早上$8$点同时出发，那么在行驶过程中，甲、乙两人何时相距$90km$？
]

答案： 解：​
(1)​设$​y_{甲}=ax​$
根据题意，得​9a=360，​解得​a=40​
故$​y_{甲}=40x(0≤x≤9)​$
图象交点的坐标为​(4，​​160)​
设$​y_{乙}=kx+b​$
根据题意得$​\begin {cases}{4k+b=160}\\{b=360}\end {cases}，$​解得$​\begin {cases}{k=-50}\\{b=360}\end {cases}​$
∴$​y_{乙}=-50x+360​$
​
(2)​令​-50x+360=0，​解得​x=7.2​
∴$​y_{甲}=40×7.2=288​$
甲与​B​地的距离为$​360-288=72(\mathrm {km})​$
​
(3)​设经过​xh，​甲、乙相距$​90\ \mathrm {km}​$
①甲、乙相遇前
​40x+50x+90=360，​解得​x=3​
此时为​11​时
②甲、乙相遇后
​40x+50x-90=360，​解得​x=5​
此时为​13​时
综上所述，甲、乙两人在​11​时或​13​时相距$​90\ \mathrm {km}​$