第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1.(1)雨滴滴下来形成雨丝,这种现象说明
(2)汽车的雨刷在挡风玻璃上刮出一个扇面,这种现象说明
(3)将三角尺绕它的一条直角边旋转一周,形成一个圆锥,这种现象说明
点动成线
. (2)汽车的雨刷在挡风玻璃上刮出一个扇面,这种现象说明
线动成面
. (3)将三角尺绕它的一条直角边旋转一周,形成一个圆锥,这种现象说明
面动成体
.
答案:
【解析】:
本题主要考查了点、线、面、体之间的关系。
(1)雨滴滴下来形成雨丝,这是点动成线的现象。当雨滴从天空落下时,它们像一个个的点,随着它们的下落,这些点连接起来形成了线,即雨丝。
(2)汽车的雨刷在挡风玻璃上刮出一个扇面,这是线动成面的现象。雨刷是一条线,当它在挡风玻璃上刮动时,这条线移动并扫过一个面,形成扇面。
(3)将三角尺绕它的一条直角边旋转一周,形成一个圆锥,这是面动成体的现象。三角尺是一个平面图形,当它绕一条边旋转时,这个面在空间中移动并形成一个立体图形,即圆锥。
【答案】:
(1)点动成线
(2)线动成面
(3)面动成体
本题主要考查了点、线、面、体之间的关系。
(1)雨滴滴下来形成雨丝,这是点动成线的现象。当雨滴从天空落下时,它们像一个个的点,随着它们的下落,这些点连接起来形成了线,即雨丝。
(2)汽车的雨刷在挡风玻璃上刮出一个扇面,这是线动成面的现象。雨刷是一条线,当它在挡风玻璃上刮动时,这条线移动并扫过一个面,形成扇面。
(3)将三角尺绕它的一条直角边旋转一周,形成一个圆锥,这是面动成体的现象。三角尺是一个平面图形,当它绕一条边旋转时,这个面在空间中移动并形成一个立体图形,即圆锥。
【答案】:
(1)点动成线
(2)线动成面
(3)面动成体
2.如图所示的几何体由
4
个面围成,其中平面有3
个,曲面有1
个;面和面相交成6
条线,其中直线有4
条,曲线有2
条;线和线相交成6
个点.
答案:
【解析】:
本题考查了学生对点、线、面、体之间关系的理解,要求学生通过观察几何体,准确数出面、线、点的数量,并区分平面与曲面、直线与曲线。
1.观察几何体可知,此几何体为半个圆柱体。
2.确定面的数量和类型:
围成几何体的各个部分就是面,数出总共有4个面。其中,平面有3个(两个底面和一个矩形侧面),曲面有1个(圆柱的侧面)。
3.确定线的数量和类型:
面与面相交形成线,数出总共有6条线。其中,直线有4条(底面的边和矩形侧面的边),曲线有2条(圆柱侧面的上下两条圆周线)。
4.确定线的交点数量:
线与线相交形成点,通过观察可知,线和线相交成6个点。
【答案】:
4;3;1;6;4;2;6
本题考查了学生对点、线、面、体之间关系的理解,要求学生通过观察几何体,准确数出面、线、点的数量,并区分平面与曲面、直线与曲线。
1.观察几何体可知,此几何体为半个圆柱体。
2.确定面的数量和类型:
围成几何体的各个部分就是面,数出总共有4个面。其中,平面有3个(两个底面和一个矩形侧面),曲面有1个(圆柱的侧面)。
3.确定线的数量和类型:
面与面相交形成线,数出总共有6条线。其中,直线有4条(底面的边和矩形侧面的边),曲线有2条(圆柱侧面的上下两条圆周线)。
4.确定线的交点数量:
线与线相交形成点,通过观察可知,线和线相交成6个点。
【答案】:
4;3;1;6;4;2;6
3.如图所示的三棱柱,它共有五个面,请写出符合下列条件的棱.(说明:每空只需写出一条即可)
(1)与棱$BB_1$平行的棱:
(2)与棱$BB_1$相交的棱:
(3)与棱$BB_1$不在同一平面内的棱:
(1)与棱$BB_1$平行的棱:
$AA_1$
; (2)与棱$BB_1$相交的棱:
$AB$
; (3)与棱$BB_1$不在同一平面内的棱:
$AC$
.
答案:
【解析】:
本题主要考查三棱柱的结构特征,特别是棱与棱之间的位置关系,包括平行、相交和异面。
(1)与棱$BB_1$平行的棱:在三棱柱中,棱$BB_1$是连接上下底面的侧棱,与它平行的棱是另一条连接上下底面的侧棱,即$AA_1$或$CC_1$。
(2)与棱$BB_1$相交的棱:棱$BB_1$与上下底面的边相交,同时也与相邻的侧棱相交。在上下底面中,与$BB_1$相交的棱有$AB$、$A_1B_1$、$BC$、$B_1C_1$;在侧棱中,由于三棱柱的侧棱互相平行,所以侧棱之间不相交,但$BB_1$与相邻的侧棱在底面相交(即与侧棱在底面的投影相交),但直接相交的棱应选上下底面的边,如$AB$。
(3)与棱$BB_1$不在同一平面内的棱:这些棱是既不与$BB_1$平行也不与$BB_1$相交的棱,即三棱柱的另外两条侧棱所对应的底面的边,如$AC$、$A_1C_1$。
【答案】:
(1)$AA_1$(或 $CC_1$)
(2)$AB$(答案不唯一)
(3)$AC$(或 $A_1C_1$)
本题主要考查三棱柱的结构特征,特别是棱与棱之间的位置关系,包括平行、相交和异面。
(1)与棱$BB_1$平行的棱:在三棱柱中,棱$BB_1$是连接上下底面的侧棱,与它平行的棱是另一条连接上下底面的侧棱,即$AA_1$或$CC_1$。
(2)与棱$BB_1$相交的棱:棱$BB_1$与上下底面的边相交,同时也与相邻的侧棱相交。在上下底面中,与$BB_1$相交的棱有$AB$、$A_1B_1$、$BC$、$B_1C_1$;在侧棱中,由于三棱柱的侧棱互相平行,所以侧棱之间不相交,但$BB_1$与相邻的侧棱在底面相交(即与侧棱在底面的投影相交),但直接相交的棱应选上下底面的边,如$AB$。
(3)与棱$BB_1$不在同一平面内的棱:这些棱是既不与$BB_1$平行也不与$BB_1$相交的棱,即三棱柱的另外两条侧棱所对应的底面的边,如$AC$、$A_1C_1$。
【答案】:
(1)$AA_1$(或 $CC_1$)
(2)$AB$(答案不唯一)
(3)$AC$(或 $A_1C_1$)
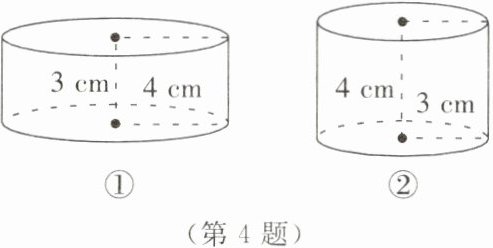
4.现将一个长为4 cm、宽为3 cm的长方形分别绕它的相邻两边所在的直线旋转一周,如图所示,得到不同的圆柱,它们的体积分别是多大?哪个圆柱的体积更大?(结果中保留$\pi$)

答案:
解:情况一:绕长所在直线旋转一周
圆柱底面半径$r = 3\,cm$,高$h = 4\,cm$
体积$V_1=\pi r^2h=\pi×3^2×4=36\pi\,cm^3$
情况二:绕宽所在直线旋转一周
圆柱底面半径$r = 4\,cm$,高$h = 3\,cm$
体积$V_2=\pi r^2h=\pi×4^2×3=48\pi\,cm^3$
$\because 48\pi>36\pi$
$\therefore$绕宽所在直线旋转得到的圆柱体积更大
答:两个圆柱体积分别为$36\pi\,cm^3$和$48\pi\,cm^3$,绕宽所在直线旋转得到的圆柱体积更大。
圆柱底面半径$r = 3\,cm$,高$h = 4\,cm$
体积$V_1=\pi r^2h=\pi×3^2×4=36\pi\,cm^3$
情况二:绕宽所在直线旋转一周
圆柱底面半径$r = 4\,cm$,高$h = 3\,cm$
体积$V_2=\pi r^2h=\pi×4^2×3=48\pi\,cm^3$
$\because 48\pi>36\pi$
$\therefore$绕宽所在直线旋转得到的圆柱体积更大
答:两个圆柱体积分别为$36\pi\,cm^3$和$48\pi\,cm^3$,绕宽所在直线旋转得到的圆柱体积更大。
5.由平的面围成的立体图形又叫作多面体,有几个面,就叫作几面体.
(1)探究:把一个多面体的顶点数记为$V$,面数记为$F$,棱数记为$E$,填表:
| 多面体 | $V$ | $F$ | $E$ | $V + F - E$ |
| --- | --- | --- | --- | --- |
| 四面体 |
| 长方体 |
| 五棱柱 |
(2)猜想:由上面的探究你能得到一个什么结论?
(3)应用:根据上述公式,想一想,会不会有一个多面体,它有10个面、30条棱、20个顶点?
(1)探究:把一个多面体的顶点数记为$V$,面数记为$F$,棱数记为$E$,填表:
| 多面体 | $V$ | $F$ | $E$ | $V + F - E$ |
| --- | --- | --- | --- | --- |
| 四面体 |
4
| 4
| 6
| 2
| | 长方体 |
8
| 6
| 12
| 2
| | 五棱柱 |
10
| 7
| 15
| 2
| (2)猜想:由上面的探究你能得到一个什么结论?
$V + F - E = 2$
(3)应用:根据上述公式,想一想,会不会有一个多面体,它有10个面、30条棱、20个顶点?
不存在
答案:
【解析】:
(1)对于四面体:顶点数$V = 4$,面数$F = 4$,棱数$E = 6$,$V + F - E=4 + 4 - 6 = 2$。
对于长方体:顶点数$V = 8$,面数$F = 6$,棱数$E = 12$,$V + F - E=8 + 6 - 12 = 2$。
对于五棱柱:顶点数$V = 10$,面数$F = 7$,棱数$E = 15$,$V + F - E=10 + 7 - 15 = 2$。
(2)通过上面的计算,可以猜想对于任何多面体,顶点数$V$、面数$F$、棱数$E$之间都满足$V + F - E = 2$,这个结论就是欧拉公式。
(3)当$V = 20$,$F = 10$,$E = 30$时,$V + F - E=20 + 10 - 30 = 0\neq2$,所以不存在这样的多面体。
【答案】:
(1)
| 多面体 | $V$ | $F$ | $E$ | $V + F - E$ |
| --- | --- | --- | --- | --- |
| 四面体 | $4$ | $4$ | $6$ | $2$ |
| 长方体 | $8$ | $6$ | $12$ | $2$ |
| 五棱柱 | $10$ | $7$ | $15$ | $2$ |
(2)$V + F - E = 2$;
(3)不存在。
(1)对于四面体:顶点数$V = 4$,面数$F = 4$,棱数$E = 6$,$V + F - E=4 + 4 - 6 = 2$。
对于长方体:顶点数$V = 8$,面数$F = 6$,棱数$E = 12$,$V + F - E=8 + 6 - 12 = 2$。
对于五棱柱:顶点数$V = 10$,面数$F = 7$,棱数$E = 15$,$V + F - E=10 + 7 - 15 = 2$。
(2)通过上面的计算,可以猜想对于任何多面体,顶点数$V$、面数$F$、棱数$E$之间都满足$V + F - E = 2$,这个结论就是欧拉公式。
(3)当$V = 20$,$F = 10$,$E = 30$时,$V + F - E=20 + 10 - 30 = 0\neq2$,所以不存在这样的多面体。
【答案】:
(1)
| 多面体 | $V$ | $F$ | $E$ | $V + F - E$ |
| --- | --- | --- | --- | --- |
| 四面体 | $4$ | $4$ | $6$ | $2$ |
| 长方体 | $8$ | $6$ | $12$ | $2$ |
| 五棱柱 | $10$ | $7$ | $15$ | $2$ |
(2)$V + F - E = 2$;
(3)不存在。
查看更多完整答案,请扫码查看


