第79页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 一个立体图形的平面展开图如图所示,这个立体图形是
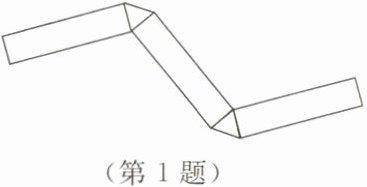
(第1题)
三棱柱
.
(第1题)
答案:
三棱柱
2. 根据下图中立体图形的展开图说出立体图形的名称.
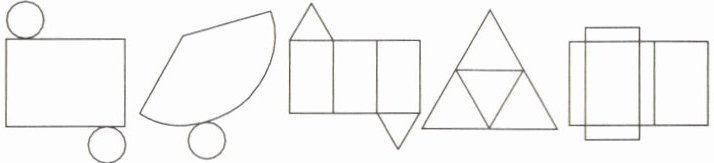
(第2题)

圆柱
圆锥
三棱柱
三棱锥
长方体
(第2题)
答案:
【解析】:本题考查对立体图形展开图的认识,通过观察不同立体图形展开图的特征,来判断对应的立体图形。
第一个图形:由两个相同的圆和一个长方形组成,这是圆柱展开图的特征,两个圆是圆柱的上下底面,长方形是圆柱的侧面展开图。
第二个图形:由一个圆和一个扇形组成,这是圆锥展开图的特征,圆是圆锥的底面,扇形是圆锥的侧面展开图。
第三个图形:由两个相同的三角形和三个长方形组成,这是三棱柱展开图的特征,两个三角形是三棱柱的上下底面,三个长方形是三棱柱的侧面展开图。
第四个图形:由四个相同的三角形组成,这是三棱锥展开图的特征,四个三角形是三棱锥的四个面。
第五个图形:由六个长方形组成,这是长方体展开图的特征,六个长方形是长方体的六个面。
【答案】:圆柱;圆锥;三棱柱;三棱锥;长方体
第一个图形:由两个相同的圆和一个长方形组成,这是圆柱展开图的特征,两个圆是圆柱的上下底面,长方形是圆柱的侧面展开图。
第二个图形:由一个圆和一个扇形组成,这是圆锥展开图的特征,圆是圆锥的底面,扇形是圆锥的侧面展开图。
第三个图形:由两个相同的三角形和三个长方形组成,这是三棱柱展开图的特征,两个三角形是三棱柱的上下底面,三个长方形是三棱柱的侧面展开图。
第四个图形:由四个相同的三角形组成,这是三棱锥展开图的特征,四个三角形是三棱锥的四个面。
第五个图形:由六个长方形组成,这是长方体展开图的特征,六个长方形是长方体的六个面。
【答案】:圆柱;圆锥;三棱柱;三棱锥;长方体
3. 如图所示,圆柱的侧面由一张长$16\pi$ cm、宽3 cm的长方形纸片围成(接缝处重叠部分忽略不计),那么该圆柱的体积是
$192\pi$或$36$
$cm^3$.
答案:
解:情况一:长方形的长为圆柱底面周长,宽为圆柱的高。
圆柱底面周长 $ C = 16\pi \, cm $,高 $ h = 3 \, cm $。
由 $ C = 2\pi r $,得底面半径 $ r = \frac{C}{2\pi} = \frac{16\pi}{2\pi} = 8 \, cm $。
圆柱体积 $ V = \pi r^2 h = \pi × 8^2 × 3 = 192\pi \, cm^3 $。
情况二:长方形的宽为圆柱底面周长,长为圆柱的高。
圆柱底面周长 $ C = 3 \, cm $,高 $ h = 16\pi \, cm $。
由 $ C = 2\pi r $,得底面半径 $ r = \frac{C}{2\pi} = \frac{3}{2\pi} \, cm $。
圆柱体积 $ V = \pi r^2 h = \pi × \left(\frac{3}{2\pi}\right)^2 × 16\pi = \pi × \frac{9}{4\pi^2} × 16\pi = 36 \, cm^3 $。
综上,该圆柱的体积是 $ 192\pi \, cm^3 $ 或 $ 36 \, cm^3 $。
圆柱底面周长 $ C = 16\pi \, cm $,高 $ h = 3 \, cm $。
由 $ C = 2\pi r $,得底面半径 $ r = \frac{C}{2\pi} = \frac{16\pi}{2\pi} = 8 \, cm $。
圆柱体积 $ V = \pi r^2 h = \pi × 8^2 × 3 = 192\pi \, cm^3 $。
情况二:长方形的宽为圆柱底面周长,长为圆柱的高。
圆柱底面周长 $ C = 3 \, cm $,高 $ h = 16\pi \, cm $。
由 $ C = 2\pi r $,得底面半径 $ r = \frac{C}{2\pi} = \frac{3}{2\pi} \, cm $。
圆柱体积 $ V = \pi r^2 h = \pi × \left(\frac{3}{2\pi}\right)^2 × 16\pi = \pi × \frac{9}{4\pi^2} × 16\pi = 36 \, cm^3 $。
综上,该圆柱的体积是 $ 192\pi \, cm^3 $ 或 $ 36 \, cm^3 $。
4. 钻石原石看起来并不起眼,但经过精心设计、切割、打磨,就会变得璀璨夺目.钻石切割是多面体截面在实际生活中的一个应用.将已经加工成三棱柱形状的钻石原石进行切割,只切一刀,切截面的形状可能是
三角形、四边形、五边形
.
答案:
解:三角形、四边形、五边形
5. 由5个棱长为1 cm的正方体组成的立体图形如图所示.
(1)该立体图形的体积是
(2)分别画出从前面和左面看到的这个立体图形的形状图.
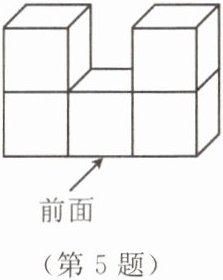
从前面看:
□ □
□ □ □
从左面看:
□ □
□ □
(1)该立体图形的体积是
5
$cm^3$,表面积是22
$cm^2$.(2)分别画出从前面和左面看到的这个立体图形的形状图.

从前面看:
□ □
□ □ □
从左面看:
□ □
□ □
答案:
(1) 5;22
(2) 从前面看:
```
□ □
□ □ □
```
从左面看:
```
□ □
□ □
```
(1) 5;22
(2) 从前面看:
```
□ □
□ □ □
```
从左面看:
```
□ □
□ □
```
6. 某校七年级同学共同制作了一个几何体模型,其展开图如图所示,则原几何体模型中与“技”字相对的是“
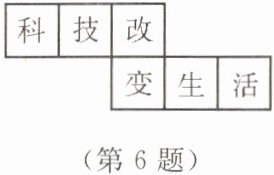
生
”字.
答案:
解:将展开图还原为正方体,"技"字所在面与"生"字所在面相对。
生
生
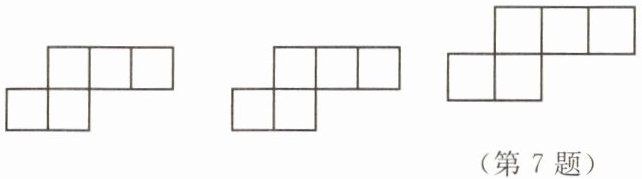
7. 如图所示,小马设计了某个产品的包装盒,由于粗心少设计了其中的一部分.请你帮他补上,使该图形能折成一个密封的正方体形状的盒子.
(1)画出两种弥补的设计图.
(2)你还有其他的弥补方案吗?尝试着画一画.
(备用图)
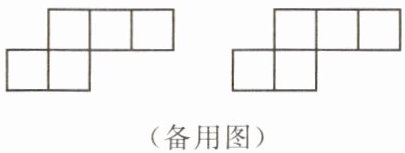
(1)画出两种弥补的设计图.
(2)你还有其他的弥补方案吗?尝试着画一画.

(备用图)

答案:
【解析】:
本题主要考查正方体的展开图,需要根据正方体的特征来补全展开图。正方体有六个面,且相对的面在展开图中是间隔出现的。
(1)第一种弥补方案:
观察已有图形,发现已经有5个面,要折成正方体,需要在右上角两个小正方形下方添加一个相连的小正方形,这样就能满足正方体展开图的特征。
第二种弥补方案:
在左上角第一个小正方形的左边添加一个相连的小正方形,也能使该图形折成一个密封的正方体形状的盒子。
(2)其他弥补方案:
还可以在备用图中,从左上角开始,把第二行第一个小正方形下面的两个小正方形整体移到第一行最右边小正方形的右边,也能构成正方体的展开图。
【答案】:
(1)图略(第一种是在右上角两个小正方形下方添加一个相连的小正方形;第二种是在左上角第一个小正方形的左边添加一个相连的小正方形)
(2)图略(如把备用图中第二行第一个小正方形下面的两个小正方形整体移到第一行最右边小正方形的右边)
本题主要考查正方体的展开图,需要根据正方体的特征来补全展开图。正方体有六个面,且相对的面在展开图中是间隔出现的。
(1)第一种弥补方案:
观察已有图形,发现已经有5个面,要折成正方体,需要在右上角两个小正方形下方添加一个相连的小正方形,这样就能满足正方体展开图的特征。
第二种弥补方案:
在左上角第一个小正方形的左边添加一个相连的小正方形,也能使该图形折成一个密封的正方体形状的盒子。
(2)其他弥补方案:
还可以在备用图中,从左上角开始,把第二行第一个小正方形下面的两个小正方形整体移到第一行最右边小正方形的右边,也能构成正方体的展开图。
【答案】:
(1)图略(第一种是在右上角两个小正方形下方添加一个相连的小正方形;第二种是在左上角第一个小正方形的左边添加一个相连的小正方形)
(2)图略(如把备用图中第二行第一个小正方形下面的两个小正方形整体移到第一行最右边小正方形的右边)
查看更多完整答案,请扫码查看


