《2025年作业本江西教育出版社七年级数学上册人教版》

1.“早穿棉袄午穿纱，围着火炉吃西瓜”描绘的是我国某地一天内气温变化较大的现象.如果该地某天早晨气温上升8℃记作+8℃，那么该地傍晚气温下降10℃应记作(D)
A.+18℃
B.-18℃
C.+10℃
D.-10℃

答案： 解：根据题意，气温上升记为“+”，则气温下降应记为“-”，所以傍晚气温下降10℃应记作-10℃。
答案：D

2.有理数$-3\frac{1}{2}$可转化为(A)
A.$-3-\frac{1}{2}$
B.$-3+\frac{1}{2}$
C.$-3÷\frac{1}{2}$
D.$-3×\frac{1}{2}$

答案： 解：$-3\frac{1}{2} = -(3 + \frac{1}{2}) = -3 - \frac{1}{2}$，故选A。

3.若单项式$xy^2$的系数为m，次数为n，则mn的值为(B)
A.4
B.3
C.2
D.0

答案： 解：单项式$xy^2$的系数$m=1$，次数$n=1+2=3$，则$mn=1×3=3$。
答案：B

4.教材中《整式的加减》一章的知识结构如图所示，则A和B分别代表的是(D)
A.整式，合并同类项
B.单项式，合并同类项
C.系数，次数
D.多项式，合并同类项

答案： 【解析】：
首先，观察知识结构图，可以看到“整式”是由“单项式”和“A”组成的，这说明“A”应该是与“单项式”并列的整式的一部分，在数学中，“整式”包括“单项式”和“多项式”，因此“A”应该代表“多项式”。
接下来，看到“整式”经过“（B）去括号”后进行“整式加减运算”。在整式的运算中，去括号是一个重要的步骤，它通常是在合并同类项之前进行的，合并同类项是整式加减运算中的一个关键步骤，它涉及到将具有相同字母部分和相同指数的项相加或相减，因此可以推断出“（B）去括号”之后应该是“合并同类项”，即“B”代表“合并同类项”。
【答案】：D

5.在应用有理数减法法则计算$-2-(-3)$时，其中需要把“-”变成“+”的是(C)
A.①②
B.①③
C.②③
D.①②③

答案： 【解析】：
首先，我们分析题目中的表达式 $-2-(-3)$。
根据有理数的减法法则，减去一个数等于加上这个数的相反数。
即 $a - b = a + (-b)$。
应用这一法则到题目中的表达式，我们有：
$-2 - (-3) = -2 + 3$。
观察这个变化过程，我们可以看到“-”变成“+”是在将 $-(-3)$ 转化为 $+3$ 的过程中发生的。
同时，我们注意到，在转化过程中，$-3$ 前面的 “-” 变成了 “+”，并且 $-3$ 变成了它的相反数 $3$，这相当于在计算过程中，将减法转化为加法，并将减数变为它的相反数。
这个过程对应了图中的步骤 ② 和 ③。
因此，需要把“-”变成“+”的是步骤 ② 和 ③。
【答案】：C。

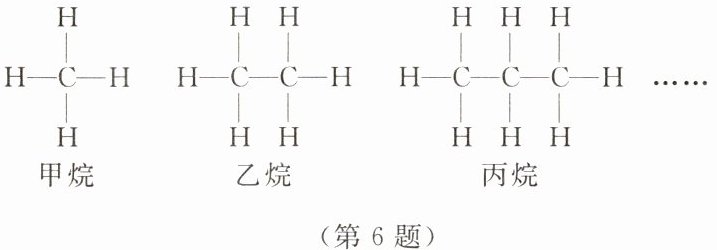
6.下图分别是有机物甲烷、乙烷、丙烷……的结构图.已知一个烷类有机物的结构与它们类似，且结构中含有n个C，则该烷类有机物的结构中含有H的个数是(D)

A.3n
B.3n+1
C.4n
D.2n+2

答案： 解：观察结构图可知：
甲烷含1个C时，H的个数为4=2×1+2；
乙烷含2个C时，H的个数为6=2×2+2；
丙烷含3个C时，H的个数为8=2×3+2；
则含n个C时，H的个数是2n+2。
答案：D

7.化简：$\left(-\frac{2}{3}\right)^2=$$\frac{4}{9}$.

答案： 解：$\left(-\frac{2}{3}\right)^2 = \left(\frac{2}{3}\right)^2 = \frac{2^2}{3^2} = \frac{4}{9}$
$\frac{4}{9}$

8.嫦娥六号探测器实现世界首次月球背面南极-艾特肯盆地采样返回.已知月球距离地球约384000km，其中用科学记数法表示384000为3.84×10⁵.

答案： 【解析】：
本题主要考察科学记数法的表示方法。
科学记数法是一种表示大数或小数的方法，其形式为 $a × 10^{n}$，其中 $1 \leq a ＜ 10$ 且 $n$ 为整数。
对于给定的数 $384000$，首先确定 $a$ 和 $n$。
将 $384000$ 转换为 $3.84 × 100000$，这里 $a = 3.84$，$n = 5$。
因此，$384000$ 用科学记数法表示为 $3.84 × 10^{5}$。
【答案】：
$3.84 × 10^{5}$

9.计算：$|-4|×(-2)=$-8.

答案： 解：$|-4|×(-2)$
$=4×(-2)$
$=-8$
$-8$

10.某超市的苹果价格如图所示，代数式7.9m的实际意义是购买m千克苹果的总价.

答案： 【解析】：本题可根据代数式中字母所代表的实际意义，结合题目中给出的苹果价格信息，来分析代数式$7.9m$的实际意义。
已知苹果的价格是$7.9$元/千克，在代数式$7.9m$中，$7.9$是苹果的单价，通常在数学中，总价$=$单价$×$数量，这里$m$可表示购买苹果的重量（千克），那么$7.9m$就表示购买$m$千克苹果的总价。
【答案】：购买$m$千克苹果的总价。