《2025年作业本江西教育出版社七年级数学上册人教版》

1. 有四个数：-3,0,1,4. 其中,负数是-3.

答案： 【解析】：
题目要求从给定的四个数中找出负数。负数定义为小于0的数。
在给定的数：-3，0，1，4中，
-3小于0，因此-3是负数；
0等于0，不是负数；
1大于0，是正数；
4大于0，是正数。
所以，给定的数中只有-3是负数。
【答案】：
-3

2. 在-8,0,9,-10 这四个数中,既不是正数,也不是负数的是0.

答案： 【解析】：
本题考查的是对正数和负数的理解。在给定的四个数-8，0，9，-10中，需要找出一个数，它既不是正数也不是负数。根据数的定义，正数是大于0的数，负数是小于0的数。而0既不大于0也不小于0，因此0既不是正数也不是负数。
【答案】：
0

3. 如果把收入30元记作+30元,那么支出20元可记作-20元.

答案： 【解析】：
题目考查了正数和负数在实际生活中的应用。在这个问题中，收入被记作正数，即“+30元”，因此，支出应该用负数来表示。这是因为在数学和财务中，正数和负数常被用来表示相反意义的量，如收入和支出、盈利和亏损等。
【答案】：
-20元。

4. 在体育课的立定跳远比赛中,以2.00m为标准,如果小东跳出了2.23m,可记作+0.23m,那么小明跳出了1.78m,可记作-0.22m.

答案： 【解析】：
题目考查正数和负数的实际应用。在这个问题中，立定跳远的成绩是以2.00m为标准的，超过这个标准的距离用正数表示，少于这个标准的距离则用负数表示。
首先，确定基准数，即标准距离，为2.00m。
接着，计算小明的跳远成绩与标准距离的差值：
$2.00m - 1.78m = 0.22m$。
由于小明的成绩少于标准距离，因此这个差值应表示为负数，即-0.22m。
所以，小明跳出了1.78m，可记作-0.22m（相对于2.00m的标准）。
【答案】：
$-0.22$

5. ①不带“-”号的数都是正数；②不带“+”号的数都是负数；③0既不是正数,也不是负数；④一个数不是正数就是负数. 以上说法中,错误的是①②④(填序号).

答案： 【解析】：
本题主要考察正数和负数的定义及性质。
① 对于不带“-”号的数，它们并不都是正数。例如，0就不带“-”号，但它不是正数。因此，此说法错误。
② 不带“+”号的数也并不都是负数。例如，0和所有的正数都不带“+”号，但它们不是负数。因此，此说法错误。
③ 0既不是正数也不是负数，这是0的定义。因此，此说法正确。
④ 一个数不仅仅是正数或负数，它还可以是0。因此，此说法错误。
综上所述，错误的说法有①、②和④。
【答案】：
①②④

6. 某超市两种品牌的面粉袋上分别标有质量为$(25±0.1)\ kg$,$(25±0.2)\ kg$的字样,从中任意拿出两袋,它们的质量最多相差______kg.
解：
1. 对于质量为$(25±0.1)\ kg$的面粉，最大质量为$25 + 0.1 = 25.1\ kg$，最小质量为$25 - 0.1 = 24.9\ kg$。
2. 对于质量为$(25±0.2)\ kg$的面粉，最大质量为$25 + 0.2 = 25.2\ kg$，最小质量为$25 - 0.2 = 24.8\ kg$。
3. 两袋面粉质量最多相差：$25.2 - 24.8 = 0.4\ kg$。
0.4

答案： 解：
1. 对于质量为$(25±0.1)\ kg$的面粉，最大质量为$25 + 0.1 = 25.1\ kg$，最小质量为$25 - 0.1 = 24.9\ kg$。
2. 对于质量为$(25±0.2)\ kg$的面粉，最大质量为$25 + 0.2 = 25.2\ kg$，最小质量为$25 - 0.2 = 24.8\ kg$。
3. 两袋面粉质量最多相差：$25.2 - 24.8 = 0.4\ kg$。
0.4

7. 《九章算术注》中有“今两算得失相反,要令正负以名之”,大意是：今有两数,若其意义相反,则分别叫作正数与负数. 若气温为零上$10\ \degreeC记作+10\ \degreeC$,则$-3\ \degreeC$表示气温为零下3°C.

答案： 【解析】：
题目考查了正数和负数的概念及其在实际问题中的应用。
根据题目描述，气温为零上的温度用正数表示，那么与之相反，气温为零下的温度应用负数表示。
题目中给出“+10°C”表示气温为零上10°C，这是一个正数表示的实际问题。
因此，对于“-3°C”，它应表示气温为零下3°C。
【答案】：
-3°C表示气温为零下3°C。

8. “产值增加-20万元”表示的意义是产值减少20万元.

答案： 【解析】：
本题考查正数和负数的意义。在一个实际问题中，正数和负数常常用来表示两种相反意义的量。
在本题中，“产值增加”通常表示为一个正数，那么“产值增加-20万元”中的负号“-”则表示与“增加”相反的意义，即“减少”。
因此，“产值增加-20万元”实际上表示“产值减少20万元”。
【答案】：
产值减少20万元。

9. 把下列各数分别填在相应的集合内. $+2025$,$-1$,$0$,$-\frac{1}{2}$,$\frac{5}{4}$,$-2\frac{3}{5}$,$+1.5$,$-32\%$,$0.7$.
正数集合：{______}；
负数集合：{______}.

答案： 【解析】：
题目要求将给定的数分类到正数集合和负数集合中。
首先，需要明确正数和负数的定义。
正数是大于零的数，负数是小于零的数。
给定的数有：$+2025$，$-1$，$0$，$-\frac{1}{2}$，$\frac{5}{4}$，$-2\frac{3}{5}$，$+1.5$，$-32\%$，$0.7$。
接下来，我们逐一判断这些数的正负性，并将它们分类到对应的集合中。
$+2025$ 是正数，因为它大于零。
$-1$ 是负数，因为它小于零。
$0$ 既不是正数也不是负数。
$-\frac{1}{2}$ 是负数，因为它小于零。
$\frac{5}{4}$ 是正数，因为它大于零。
$-2\frac{3}{5}$ 是负数，可以转化为$-\frac{13}{5}$，因为它小于零。
$+1.5$ 是正数，因为它大于零。
$-32\%$ 是负数，因为它小于零（$ -32\%=-\frac{32}{100}=-\frac{8}{25}$）。
$0.7$ 是正数，因为它大于零。
【答案】：
正数集合：{$+2025$，$\frac{5}{4}$，$+1.5$，$0.7$}；
负数集合：{$-1$，$-\frac{1}{2}$，$-2\frac{3}{5}$，$-32\%$}。

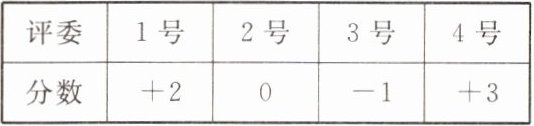
10. 某次唱歌比赛由4位评委打分决定选手能否晋级. 规定每位评委能打的满分是10分. 把6分记为0分,超过的用正数表示,不足的用负数表示；选手的总分达到25分可以晋级. 5号选手小明的得分情况如下表所示. 小明的最后得分是多少？能否晋级？

答案： 解：每位评委以6分为基准，小明各评委实际得分为：
1号：6 + 2 = 8分
2号：6 + 0 = 6分
3号：6 + (-1) = 5分
4号：6 + 3 = 9分
总分：8 + 6 + 5 + 9 = 28分
28 ＞ 25
答：小明的最后得分是28分，能晋级。