《2025年作业本江西教育出版社七年级数学上册人教版》

1. 单项式$-9\pi x^{6}y$的系数是$-9\pi$,次数是7。

答案： 【解析】：
本题主要考查了单项式的系数与次数的定义。单项式中的数字因数叫做这个单项式的系数，一个单项式中，所有字母的指数的和叫做这个单项式的次数。
对于单项式$-9\pi x^{6}y$，
系数：单项式中的数字因数是$-9\pi$，所以系数是$-9\pi$。
次数：需要计算所有字母的指数和。在这里，$x$的指数是$6$，$y$的指数是$1$（因为$y$可以看作是$y^1$），所以次数是$6+1=7$。
【答案】：
系数是$-9\pi$，次数是$7$。

2. 某飞机在无风时的航速是$a$ km/h,风速为20 km/h。飞机顺风飞行了4 h后又逆风飞行了3 h,飞机共飞行了7a + 20km。

答案： 解：飞机顺风速度为$(a + 20)$km/h，顺风飞行4h的路程为$4(a + 20)$km；逆风速度为$(a - 20)$km/h，逆风飞行3h的路程为$3(a - 20)$km。
共飞行路程为：$4(a + 20) + 3(a - 20)$
$=4a + 80 + 3a - 60$
$=7a + 20$
$7a + 20$

3. 如果$x^{2}-3x= 2$,那么多项式$-2x^{2}+6x+9$的值是5。

答案： 【解析】：
本题主要考查代数式的代入法求解。
首先，我们已知 $x^{2} - 3x = 2$，
接下来，我们需要求多项式 $-2x^{2} + 6x + 9$ 的值。
观察多项式，我们可以发现它可以被重写为 $-2(x^{2} - 3x) + 9$，
这样，我们就可以直接将 $x^{2} - 3x = 2$ 代入这个表达式中，
进行计算。
【答案】：
解：
∵ $x^{2} - 3x = 2$，
∴ $-2x^{2} + 6x + 9$
$= -2(x^{2} - 3x) + 9$
$= -2 × 2 + 9$
$= -4 + 9$
$= 5$
故答案为：5。

4. 已知多项式$(2x^{2}+ax-y+6)-(bx^{2}-2x+5y-1)$。
(1)若多项式的值与$x$的取值无关,求$a,b$的值。
(2)在(1)的条件下,先化简多项式$2(a^{2}-ab+b^{2})-(a^{2}+ab+2b^{2})$,再求它的值。

答案：
(1)解：$(2x^{2}+ax-y+6)-(bx^{2}-2x+5y-1)$
$=2x^{2}+ax-y+6-bx^{2}+2x-5y+1$
$=(2-b)x^{2}+(a+2)x-6y+7$
因为多项式的值与$x$的取值无关，所以$2-b=0$，$a+2=0$，解得$a=-2$，$b=2$。
(2)解：$2(a^{2}-ab+b^{2})-(a^{2}+ab+2b^{2})$
$=2a^{2}-2ab+2b^{2}-a^{2}-ab-2b^{2}$
$=a^{2}-3ab$
当$a=-2$，$b=2$时，原式$=(-2)^{2}-3×(-2)×2=4 + 12=16$。

5. 如图所示,正方形$ABCD和正方形ECGF的边长分别为a$和4。
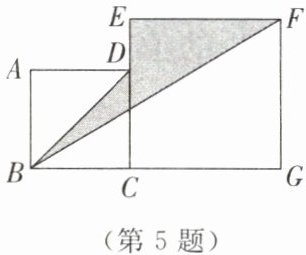
(1)写出表示阴影部分面积的代数式(结果要求化简)。
(2)求$a= 3$时阴影部分的面积。

答案：
(1)解：由题意得，阴影部分面积 = 正方形ABCD面积 + 正方形ECGF面积 - 三角形ABD面积 - 三角形BGF面积。
正方形ABCD面积 = $a^2$，正方形ECGF面积 = $4^2 = 16$，
三角形ABD面积 = $\frac{1}{2}a^2$，三角形BGF面积 = $\frac{1}{2}(a + 4)×4 = 2(a + 4)$，
阴影部分面积 = $a^2 + 16 - \frac{1}{2}a^2 - 2(a + 4) = \frac{1}{2}a^2 - 2a + 8$。
(2)解：当$a = 3$时，阴影部分面积 = $\frac{1}{2}×3^2 - 2×3 + 8 = \frac{9}{2} - 6 + 8 = \frac{13}{2}$。

6. 甲三角形的周长为$3a^{2}-6b+8$。乙三角形的第一条边长为$a^{2}-2b$,第二条边长为$a^{2}-3b$,第三条边比第二条边短$a^{2}-2b-5$。
(1)求乙三角形第三条边的长。
(2)甲、乙两个三角形的周长哪个大？试说明理由。

答案： 【解析】：
本题主要考察整式的加减运算和代数式的比较。
(1) 根据题目描述，乙三角形的第三条边长可以通过第二条边长减去给定的表达式来求得。
(2) 要比较甲、乙两个三角形的周长，首先需要求出乙三角形的周长，然后将其与甲三角形的周长进行比较。
【答案】：
(1) 解：
乙三角形的第三条边长为
$(a^{2} - 3b) - (a^{2} - 2b - 5)$
$= a^{2} - 3b - a^{2} + 2b + 5$
$= -b + 5$
答：乙三角形的第三条边长为 $-b + 5$。
(2) 解：
乙三角形的周长为
$(a^{2} - 2b) + (a^{2} - 3b) + (-b + 5)$
$= 2a^{2} - 6b + 5$
甲三角形的周长为 $3a^{2} - 6b + 8$，
比较两者，有
$(3a^{2} - 6b + 8) - (2a^{2} - 6b + 5)$
$= a^{2} + 3$
由于 $a^{2} + 3 ＞ 0$（因为 $a^{2}$ 总是非负的，且3为正数），
所以甲三角形的周长大于乙三角形的周长。
答：甲三角形的周长大于乙三角形的周长。