《2025年作业本江西教育出版社七年级数学上册人教版》

1. 如$3= \frac{3}{1}$,$0= \frac{0}{1}$,$-1.5= -\frac{3}{2}$等,可以写成整数之比（或两个整数的比，且分母不为0）形式的数称为有理数.

答案： 解：整数之比（或两个整数的比，且分母不为0）

2. 在数$\frac{1}{4}$,$-3$,$5$,$0$,$1.8$中,属于正整数的是5.

答案： 【解析】：
题目要求在给定的数中找出属于正整数的数。
首先，需要明确正整数的定义：大于0且带有正号的整数。
给定的数有：$\frac{1}{4}$，$-3$，$5$，$0$，$1.8$。
其中，$\frac{1}{4}$是一个分数，不是整数；
$-3$是一个负整数，不是正整数；
$5$是一个大于0的整数，是正整数；
$0$是整数，但不是正整数；
$1.8$是一个小数，不是整数。
因此，属于正整数的数只有$5$。
【答案】：
$5$

3. 有理数$1.7$,$-17$,$0$,$-\frac{5}{7}$,$-0.003$,$2025$,$\frac{9}{2}$,$-1$中,负数有4个,负整数有2个,非负数有4个.

答案： 【解析】：
题目要求确定给定数列中的负数、负整数和非负数的个数。
首先，需要明确有理数的几种分类：
负数：小于0的数。
负整数：小于0的整数。
非负数：大于或等于0的数。
接下来，逐一判断每个数的类别：
$1.7$：正小数，属于非负数。
$-17$：负整数，属于负数。
$0$：非负整数，属于非负数。
$-\frac{5}{7}$：负分数，属于负数。
$-0.003$：负小数，属于负数。
$2025$：正整数，属于非负数。
$\frac{9}{2}$：正分数，属于非负数。
$-1$：负整数，属于负数。
统计各类数的个数：
负数有4个（$-17$，$-\frac{5}{7}$，$-0.003$，$-1$）。
负整数有2个（$-17$，$-1$）。
非负数有4个（$1.7$，$0$，$2025$，$\frac{9}{2}$）。
【答案】：
负数有 $4$ 个，负整数有 $2$ 个，非负数有 $4$ 个。

4. 有下列说法：①$-5.56$既是负数、分数,也是有理数；②正整数和负整数统称为整数；③$-2025$既是负数,也是整数,但不是有理数；④自然数是整数. 其中正确的是①④(填序号).

答案： 【解析】：
本题主要考察有理数的概念及分类。
① $-5.56$ 是一个负数，因为它小于0；同时，它可以表示为分数形式 $-\frac{556}{100}$ 或简化为其他形式，所以它也是分数；所有的分数都是有理数，因此，$-5.56$ 是有理数。所以①正确。
② 正整数和负整数以及0统称为整数。原说法中遗漏了0，所以②错误。
③ $-2025$ 是一个负数，因为它小于0；同时，它也是一个整数；所有的整数都是有理数，因此，$-2025$ 是有理数。原说法中“不是有理数”是错误的，所以③错误。
④ 自然数（包括0和所有正整数）都是整数的一部分。所以④正确。
综上所述，正确的说法是①和④。
【答案】：
①④

5. 有下列各数：①$-5$；②$-\frac{22}{7}$；③$0$；④$+1.5$；⑤$0.1010010001…$(每两个$1之间依次多一个0$)；⑥$-30\%$. 其中是有理数的是①②③④⑥(填序号).

答案： 解：有理数是整数（正整数、0、负整数）和分数的统称。
①$-5$是负整数，是有理数；
②$-\frac{22}{7}$是分数，是有理数；
③$0$是整数，是有理数；
④$+1.5$是有限小数，可化为分数，是有理数；
⑤$0.1010010001…$（每两个1之间依次多一个0）是无限不循环小数，不是有理数；
⑥$-30\%$可化为$-\frac{3}{10}$，是分数，是有理数。
故是有理数的是①②③④⑥。
答案：①②③④⑥

小明是七年级学生,身高160 cm,体重41.5kg. 他每天坚持晨练30 min,即使冬天的早上温度只有-5°C,他也坚持锻炼. 他沿着学校操场上400 m的跑道跑3圈,共1.2km,用时大约15min,跑步时间占整个晨练时间的$\frac{1}{2}$.

答案： 【解析】：
这个问题主要考察的是对有理数概念的理解以及单位换算。题目中给出了几个数字，需要根据上下文选择合适的数字填入空白处。
首先，体重通常用整数或者小数来表示，给出的数字中，$15$和$41.5$可能是体重。由于$41.5$对于七年级学生的体重来说可能偏重，所以选择$41.5$作为体重的数值较为合理，但考虑到学生实际，这里更可能是$15$的倍数或者接近的数值表示体重的常用单位（一般是kg），因此选择$41.5$附近的整数$15$的2倍多即符合学生体重，所以第一个空填$41.5$的简化考虑即填$41.5$（实际生活中学生体重可能各异，但根据题目数字判断）。
接着，温度通常用负数来表示零下的温度，所以$-5$应该填入表示温度的空白处。
然后，距离通常用长度单位来表示，给出的数字中，$400m$的跑道跑$3$圈就是$1200m$，换算成$km$就是$1.2km$。
时间则用分钟来表示，每天坚持晨练$30min$，所以时间相关的空白处应填入$30$的约数或者与$30$有关的数，题目中$30min$晨练中跑步的时间需要估算，但根据后文“跑步时间占整个晨练时间的......”可以结合后文给出的分数$\frac{1}{2}$（如果考虑跑步和其他活动时间分配），或者简单理解为跑步用时约晨练总时长的一部分，这里直接根据跑3圈$400m$跑道的合理时间判断，可以近似看作跑步时间接近但小于$30min$，而题目中只有$15$和$30$两个与时间可能相关的数字（$1.2$和$\frac{1}{2}$显然不是分钟数），考虑到是3圈且是晨练的一部分，选择$15$作为跑步的近似时间（实际可能因人而异，但根据题目选项和常识判断）。不过此处按照题目设计的逻辑直接取与晨练时间$30min$相关的且未使用的数字$15$的2倍关系对应晨练中的跑步时间理解（即如果跑步占一半时间则正好为$15× 2 ÷ 2 =15$的逻辑对应，但直接理解为题目设计的对应关系即可），所以直接填$15$。
最后，跑步时间占整个晨练时间的比例应该用分数来表示，给出的数字中，$\frac{1}{2}$可以表示这个比例。
【答案】：
$41.5$；$-5$；$1.2$；$15$；$\frac{1}{2}$。

7. 指出下列各数中的正有理数、负有理数、整数.$+8.5$,$-3\frac{1}{2}$,$0.3$,$0$,$-3.4$,$-9$,$3.14$,$4\frac{1}{3}$,$-3.\dot{1}\dot{7}$,$-2$,$0.\dot{6}\dot{7}$.

答案： 【解析】：
本题主要考查了有理数的分类，包括正有理数、负有理数和整数的识别。
首先，需要明确什么是有理数。
有理数是可以表示为两个整数之比的数，即形如$\frac{a}{b}$的数，其中$a$和$b$是整数，且$b \neq 0$。
正有理数是大于0的有理数，负有理数是小于0的有理数，整数包括正整数、0和负整数。
接下来，逐一判断给出的数属于哪一类：
$+8.5$ 是大于0的有理数，所以它是正有理数。
$-3\frac{1}{2}$ 是小于0的有理数，所以它是负有理数。
$0.3$ 是大于0的有理数，所以它是正有理数。
$0$ 是整数。
$-3.4$ 是小于0的有理数，所以它是负有理数。
$-9$ 是小于0的整数，所以它是负有理数（同时也是整数）。
$3.14$ 是大于0的有理数，所以它是正有理数。
$4\frac{1}{3}$ 是大于0的有理数，所以它是正有理数。
$-3.\dot{1}\dot{7}$ 是小于0的有理数（循环小数也是有理数），所以它是负有理数。
$-2$ 是小于0的整数，所以它是负有理数（同时也是整数）。
$0.\dot{6}\dot{7}$ 是大于0的有理数（循环小数也是有理数），所以它是正有理数。
【答案】：
正有理数：$\{+8.5, 0.3, 3.14, 4\frac{1}{3}, 0.\dot{6}\dot{7}\}$；
负有理数：$\{-3\frac{1}{2}, -3.4, -3.\dot{1}\dot{7}, -2, -9\}$；
整数：$\{0, -2, -9\}$。

8. 所有的正数组成正数集合,所有的负数组成负数集合,所有的整数组成整数集合. 下图中的三个圈分别表示负数集合、整数集合和正数集合.

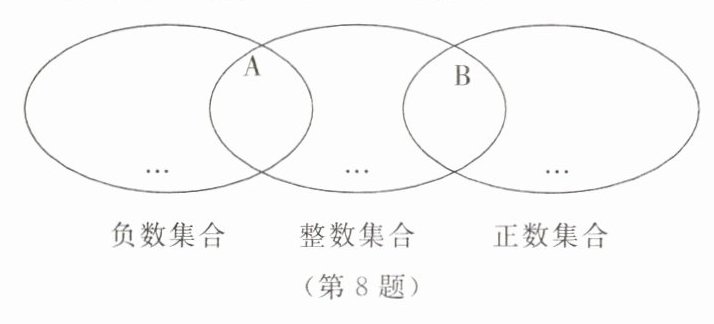
(1)请将下列各数填入图中适当的位置.
负数集合：$-0.1$，$-3$，$-5\frac{1}{2}$，$-2025$
整数集合：$-3$，$0$，$+54$，$-2025$
正数集合：$1$，$\frac{27}{7}$，$9.25$，$+54$
(2)图中两个圈的公共部分,A区域表示______集合；B区域表示______集合.
负整数正整数

答案： 【解析】：
本题考查正数，负数，整数的概念，需要正确理解正数、负数和整数的定义，并根据这些定义将给定的数分类填入图中，需要理解图中不同区域所表示的集合含义。
（1）正数是大于0的数，包括正整数和正分数；负数是小于0的数，包括负整数和负分数；整数包括正整数、0、负整数，根据这些定义来对给定的数进行分类。
（2）A区域是负数集合和整数集合的公共部分，即既是负数又是整数的数组成的集合，也就是负整数集合；B区域是正数集合和整数集合的公共部分，即既是正数又是整数的数组成的集合，也就是正整数集合。
【答案】：
(1)从左到右，从上到下，
负数集合：$-0.1$，$-3$，$-5\frac{1}{2}$，$-2025$
整数集合：$-3$，$0$，$+54$，$-2025$
正数集合：$1$，$\frac{27}{7}$，$9.25$，$+54$
(2)A区域表示负整数集合；B区域表示正整数集合。