《2025年作业本江西教育出版社七年级数学上册人教版》

1. 计算：$(-2)^2 + (-2) × 2 = $0.

答案： 解：$(-2)^2 + (-2) × 2$
$=4 + (-4)$
$=0$

2. 若有理数$a,b$互为相反数,$c,d$互为倒数,则$(a+b)^{2026} - (-cd)^{2025} = $1.

答案： 解：因为有理数$a$，$b$互为相反数，所以$a + b = 0$。
因为$c$，$d$互为倒数，所以$cd = 1$。
则$(a + b)^{2026} - (-cd)^{2025} = 0^{2026} - (-1)^{2025}$
$= 0 - (-1)$
$= 1$
1

3. 某个数值转换机的示意图如右图所示.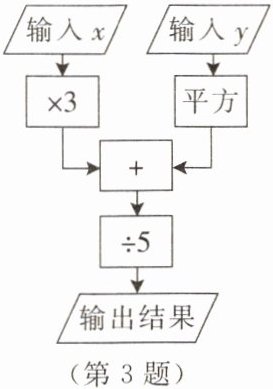
若输入$x$的值为2,输入$y的值为-2$,则输出结果为______.2

答案： 【解析】：
本题可根据数值转换机的运算顺序，先分别计算出$x$乘以$3$的结果以及$y$平方的结果，再将这两个结果相加，最后用相加的和除以$5$，即可得到输出结果。
已知输入$x$的值为$2$，输入$y$的值为$-2$，按照数值转换机的运算顺序逐步计算：
计算$x$乘以$3$的值：将$x = 2$代入$x×3$，可得$2×3 = 6$。
计算$y$平方的值：将$y = -2$代入$y^2$，根据乘方的定义，$(-2)^2=(-2)×(-2)= 4$。
计算上述两个结果的和：将$6$与$4$相加，可得$6 + 4 = 10$。
计算最终输出结果：用$10$除以$5$，即$10÷5 = 2$。
【答案】：
$2$

4. 我们常用的数是十进制数,计算机程序使用的是二进制数(只有数码0和1),它们两者之间可以互相换算. 若规定：任何一个非0数的0次幂都等于1(如$2^0 = 1$,$3^0 = 1$),那么二进制$(101)_2$,$(1011)_2换算成十进制数为(101)_2 = 1 × 2^2 + 0 × 2^1 + 1 × 2^0$；$(1011)_2 = 1 × 2^3 + 0 × 2^2 + 1 × 2^1 + 1 × 2^0$. 按此方式,将二进制数$(11001)_2$换算成十进制数的结果是______25.

答案： 解：$(11001)_2 = 1×2^4 + 1×2^3 + 0×2^2 + 0×2^1 + 1×2^0$
$= 1×16 + 1×8 + 0×4 + 0×2 + 1×1$
$= 16 + 8 + 0 + 0 + 1$
$= 25$
答案：25

5. 已知$a,b$为有理数,且$|a + 2| + (b - 3)^2 = 0$,则$a^b - ab = $-2.

答案： 解：因为$|a + 2| + (b - 3)^2 = 0$，且$|a + 2| \geq 0$，$(b - 3)^2 \geq 0$，所以$a + 2 = 0$，$b - 3 = 0$，解得$a = -2$，$b = 3$。
则$a^b - ab = (-2)^3 - (-2)×3 = -8 + 6 = -2$。
$-2$

6. 计算.
(1)$(-5)^2 × \left(-\frac{3}{5}\right) + 32 ÷ (-2^2) × \left(-1\frac{1}{4}\right)$;
(2)$(-1)^4 + (-2)^3 × \left(-\frac{1}{2}\right) - (-3^2) - |-1 - 5|$.

答案： 【解析】：
本题主要考查了乘方、乘除法、加减法以及分数和小数的运算。
(1) 对于第一个表达式，首先计算乘方，然后进行乘除运算，最后进行加减运算。
(2) 对于第二个表达式，同样首先计算乘方，注意到$-3^2$与$(-3)^2$的区别，$-3^2$表示$-(3^2)$，然后进行乘除运算，绝对值运算，最后进行加减运算。
【答案】：
(1)
解：
$\begin{aligned}(-5)^2 × \left(-\frac{3}{5}\right) + 32 ÷ (-2^2) × \left(-1\frac{1}{4}\right) \\= 25 × \left(-\frac{3}{5}\right) + 32 ÷ (-4) × \left(-\frac{5}{4}\right) \\= -15 + (-8) × \left(-\frac{5}{4}\right) \\= -15 + 10 \\= -5\end{aligned}$
(2)
解：
$\begin{aligned}(-1)^4 + (-2)^3 × \left(-\frac{1}{2}\right) - (-3^2) - |-1 - 5| \\= 1 + (-8) × \left(-\frac{1}{2}\right) - (-9) - | -6| \\= 1 + 4 + 9 - 6 \\= 8\end{aligned}$

7. 观察下列三行数：
$-2,4,-8,16,-32,64,…$;①
$1,7,-5,19,-29,67,…$;②
$4,-8,16,-32,64,-128,…$;③
(1)第①行中的数可以看成按什么规律排列？
(2)第②③行中的数与第①行中的数分别有什么关系？
(3)取每行中的第10个数,计算这三个数的和.

答案：
(1) 第①行数的规律为：后一个数是前一个数乘以-2，第n个数为$(-2)^n$。
(2) 第②行中的每个数是第①行中对应数加3；第③行中的每个数是第①行中对应数乘以-2。
(3) 第①行第10个数：$(-2)^{10}=1024$
第②行第10个数：$1024 + 3 = 1027$
第③行第10个数：$1024×(-2) = -2048$
三个数的和：$1024 + 1027 + (-2048) = 3$
答：这三个数的和为3。