《2025年作业本江西教育出版社七年级数学上册人教版》

9. 小林到某纸箱厂参加社会实践,该厂计划用50张白板纸制作某种型号的长方体纸箱,如图所示。每张白板纸有A,B,C三种剪裁方法,其中A种裁法：裁成4个侧面；B种裁法：裁成3个侧面与2个底面；C种裁法：裁成2个侧面与4个底面。已知4个侧面和2个底面恰好能做成一个纸箱。设按A种方法剪裁的白板纸有$x$张,按B种方法剪裁的白板纸有$y$张。

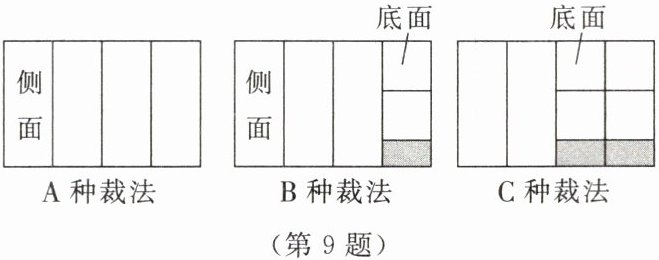
(1)按C种方法剪裁的白板纸有50 - x - y张。(用含$x$,$y$的式子表示)
(2)将50张白板纸剪裁完后,一共可以裁出多少个侧面与多少个底面？(用含$x$,$y$的式子表示,结果要化简)
解：侧面：$4x + 3y + 2(50 - x - y) = 2x + y + 100$（个）；
底面：$2y + 4(50 - x - y)= - 4x - 2y + 200$（个）。
答：一共可以裁出$(2x + y + 100)$个侧面与$( - 4x - 2y + 200)$个底面。

答案： 【解析】：
(1)观察图形可知，按A种方法剪裁的白板纸有$x$张,按B种方法剪裁的白板纸有$y$张，根据总张数为50张，即可得出按C种方法剪裁的白板纸有$(50 - x - y)$张。
(2)先根据A、B、C三种裁法一张白板纸各裁出侧面、底面的个数，分别乘以按A、B、C三种方法剪裁的白板纸的张数，再把所得的积相加，即可得出答案。
【答案】：
(1)$50 - x - y$
(2)解：侧面：$4x + 3y + 2(50 - x - y) = 2x + y + 100$（个）；
底面：$2y + 4(50 - x - y)= - 4x - 2y + 200$（个）。
答：一共可以裁出$(2x + y + 100)$个侧面与$( - 4x - 2y + 200)$个底面。

10. 一个四位数,如果它的千位数字与个位数字相同,百位数字与十位数字相同,那么称这个四位数为“对称数”,如5225,3113就是“对称数”。
(1)若一个“对称数”的个位数字为$a$,十位数字为7,则用含$a$的代数式表示该“对称数”为$1001a + 770$。
(2)判断任意一个四位“对称数”能否被11整除,若能,请用字母表示该数并说明理由；若不能,请举出反例。
能。理由：设“对称数”的个位数字为$a$，十位数字为$b$，则这个“对称数”可以表示为$1001a + 110b$，即$11(91a + 10b)$。由于$a$，$b$都是整数，因此$91a + 10b$也是整数，所以任意一个四位“对称数”都能被11整除。

答案： 【解析】：
本题主要考查代数式的表示和整除的判断。
(1) 对于一个“对称数”，若其个位数字为$a$，十位数字为7，则根据“对称数”的定义，其百位数字也为7，千位数字为$a$。因此，这个“对称数”可以表示为：$1000a + 700 + 70 + a = 1001a + 770$。
(2) 要判断任意一个四位“对称数”能否被11整除，我们可以设这个“对称数”的个位数字为$a$，十位数字为$b$。则根据“对称数”的定义，这个数可以表示为：$1000a + 100b + 10b + a = 1001a + 110b$。提取公因数11，得到：$1001a + 110b = 11(91a + 10b)$。由于$a$和$b$都是整数，因此$91a + 10b$也是整数。所以，任意一个四位“对称数”都可以被11整除。
【答案】：
(1) $1001a + 770$
(2) 能。理由：设“对称数”的个位数字为$a$，十位数字为$b$，则这个“对称数”可以表示为$1001a + 110b$，即$11(91a + 10b)$。由于$a$，$b$都是整数，因此$91a + 10b$也是整数，所以任意一个四位“对称数”都能被11整除。